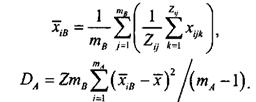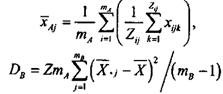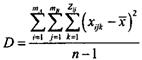Вибіркова сукупність значень коефіцієнта проникності нафтоносного пласта, що визначалися у 6 свердловинах за даними лабораторних досліджень керна

		№ п/п	№ варіанта
			1	2	3	4	5	6	7	8	9	10
Свердловина №1	паралельно	1	10	19	10	13	13	12	13	24	24	25
		2	16	24	13	8	10	17	11	18	24	12
		3	16	11	10	23	15	22	19	8	11	10
		4	13	21	14	24	24	14	8	9	23	9
	перпендикулярно	5	18	20	22	21	18	9	24	23	13	11
		6	13	16	16	25	19	15	13	20	13	21
		7	23	8	12	15	8	19	23	21	12	18
		8	19	13	23	22	21	20	12	10	16	22
Свердловина №2	паралельно	9	17	18	20	8	11	14	9	19	12	11
		10	24	10	20	11	17	21	17	14	15	18
		11	11	15	13	24	9	24	9	24	20	23
		12	15	10	9	17	13	18	22	10	8	20
	перпендикулярно	13	19	16	19	16	18	25	10	8	22	23
		14	16	10	23	20	15	13	18	19	24	12
		15	14	16	11	12	14	22	22	13	12	22
		16	11	24	12	22	21	18	13	17	11	11
Свердловина №3	паралельно	17	25	10	16	14	10	13	22	15	14	23
		18	9	17	15	22	15	22	10	16	17	20
		19	10	19	14	15	23	18	15	22	13	17
		20	20	11	15	11	16	14	16	21	10	14
	перпендикулярно	21	15	18	20	13	19	17	20	11	16	19
		22	10	20	24	15	11	10	23	15	8	22
		23	23	14	23	23	20	13	8	22	13	11
		24	10	11	11	23	21	15	21	20	21	19
Свердловина №4	паралельно	25	19	20	9	18	25	19	17	24	20	8
		26	20	18	11	9	22	9	23	22	11	21
		27	21	15	19	20	11	10	15	10	14	12
		28	11	15	13	9	8	11	13	16	10	21
	перпендикулярно	29	10	12	9	18	24	13	22	15	10	13
		30	16	19	21	24	16	19	15	21	19	10
		31	16	19	20	20	13	13	15	17	19	19
		32	22	12	11	10	11	20	24	15	8	17
Свердловина №5	паралельно	33	8	17	11	14	9	23	17	21	10	15
		34	21	15	13	11	9	15	20	14	12	12
		35	19	20	18	9	13	23	20	12	16	15
		36	19	23	13	12	23	9	9	8	19	19
	перпендикулярно	37	21	23	21	17	18	17	8	18	9	25
		38	21	13	19	20	12	21	9	24	24	23
		39	22	24	10	21	10	18	21	16	9	22
		40	20	20	10	8	9	14	23	12	15	9
Свердловина №6	паралельно	41	9	15	10	9	23	16	20	21	15	19
		42	17	20	23	13	18	19	21	19	18	19
		43	11	14	21	15	11	25	19	11	19	16
		44	9	17	20	23	19	11	12	15	8	15
	перпендикулярно	45	18	22	19	11	17	16	17	18	23	21
		46	18	9	11	14	21	8	15	8	9	20
		47	24	24	22	19	12	20	17	8	16	18
		48	10	8	24	12	12	12	11	10	13	21

Для умов прикладу:

– сума групових дисперсій – ΣD_ij=290,6.

–  значення (Z_ij – 1)=4 – 1=3.

– значення ΣΣ(Z_ij – 1)=n – m_A·m_B=48 – 6·2=36.

Тоді внутрішньогрупова дисперсія в усій вибірковій сукупності, що не пов’язана із впливом факторів А і В, для умов даного прикладу буде складати D_вг=3·290,6/36=24,2.

Числове значення відповідної суми квадратів відхилень становить S_вг=D_вг(n – m_А·m_В)=24,2·(48 – 2·6)=872.

Таблиця 7.2

Таблиця 7.3

11. Оцінка дисперсії D_А, яка характеризує мінливість величини Х під впливом лише фактора А, базується на сумі квадратів відхилень середніх значень х_іВ (математичне очікування для значень коефіцієнта проникності для кожної свердловини, фактором напряму відбору нехтуємо) по окремих рівнях фактора А від загального середнього х_ср.

Розраховані середні значення х_іВ по окремих рівнях фактора А та сума квадратів відхилень х_іВ від загального середнього х_ср для умов приклада наведено у табл. 7.4.

Таблиця 7.4

Тоді значення дисперсії D_А, яка характеризує мінливість величини Х під впливом лише фактора А для умов прикладу складає
D_А=4·2·22,76/(6 – 1)=36,4.

Числове значення відповідної суми квадратів відхилень становить S_А=D_А·(m_А–1)=36,4·(6 – 1)=182.

12. Оцінка дисперсії D_В, яка характеризує мінливість величини Х під впливом лише фактора В, базується на сумі квадратів відхилень середніх значень х_Аj (математичне очікування для значень коефіцієнта проникності, визначеної перпендикулярно і паралельно до нашарування) по окремих рівнях фактора В від загального середнього х_ср.

Розраховані середні значення х_Аj по окремих рівнях фактора А та сума квадратів відхилень х_Аj від загального середнього х_ср для умов приклада наведено у табл. 7.5.

Таблиця 7.5

Тоді значення дисперсії D_В, яка характеризує мінливість величини Х під впливом лише фактора В для умов приклада складає

D_В=4·6·6,57/(2 – 1)=157,7.

Числове значення відповідної суми квадратів відхилень становить S_В=D_В·(m_В – 1)=157,7·(2 – 1)=158.

13. Оцінка дисперсії D_АВ, яка характеризує мінливість величини Х під впливом факторів А і В, базується на сумі квадратів відхилень середніх значень х_іj для кожної комбінації рівнів факторів А і В від загального середнього х_ср.

Розраховані середні значення х_іj та сума квадратів відхилень х_іj від загального середнього х_ср для умов приклада наведено у табл. 7.6.

Тоді значення дисперсії D_АВ, яка характеризує мінливість величини Х під впливом факторів А і В для умов приклада складає
D_АВ=122,81/((6 – 1)·(2 – 1))=30,3.

Числове значення відповідної суми квадратів відхилень становить S_АВ=D_АВ(m_А – 1)(m_В – 1)=24,6·(6 – 1)·(2 – 1)=151.

Таблиця 7.6

14. Загальна дисперсія вибірки D визначається за формулою

Для умов приклада загальна дисперсія складає D=29,00 (визначено за допомогою функції «ДИСП» для усієї вибірки ВВ проникностей).

Загальна сума квадратів відхилень становить
S=D(n – 1)=29,0·(48 – 1)=1363.

Виконуємо перевірку розрахунків. Якщо все було вірно зроблено, то S=S_А+S_В+S_вг+S_АВ=182+158+151+872=1363.

15. Визначаємо критерій Фішера для вибірок, згрупованих за факторами А, В, АВ.

F_А=D_А/D_вг=36,4/24,2=1,5;

F_В=D_В/D_вг=157,7/24,2=6,5;

F_АВ=D_АВ/D_вг=30,3/24,2=1,25.

16. Визначаємо критичні значення критерію Фішера за таблицею 5.1 для рівня істотності 0,05.

Критичне значення для фактора А для рівня істотності 0,05 та ступеня вільності m₁=m_А – 1=6 – 1=5 і m₂=n – m_А·m_В=48 – 6·2=36 буде складати F_Акр=2,48.

Критичне значення для фактора В для рівня істотності 0,05 та ступеня вільності m₁=m_В – 1=2 – 1=1 і m₂=n – m_А·m_В=48 – 6·2=36 буде складати F_Вкр=4,11.

Критичне значення для взаємодії факторів А і В для рівня істотності 0,05 та ступеня вільності m₁=(m_А – 1)·(m_В – 1)=(6 – 1)·(2 – 1)=5 і m₂=n – m_А·m_В=48 – 6·2=36 буде складати F_Вкр=2,48.

17. Робимо відповідні висновки щодо виконаних розрахунків.

17.1. Фактичне значення F_А=1,5<F_Акр=2,48 менше за критичне, отже положення свердловини на родовищі (фактор А) не має істотного впливу на проникність керна.

17.2. Фактичне значення F_В=6,5>F_Вкр=4,11 більше за критичне, отже просторова орієнтація (фактор В) має істотний вплив на проникність керна.

17.3. Фактичне значення F_АВ=1,5<F_АВкр=2,48 менше за критичне, отже взаємодія факторів А і В не має істотного впливу на проникність керна.

18. Дані розрахунки можливо виконати автоматично, використавши функцію «Двухфакторный дисперсионный анализ с повторениями» надбудови «Анализ данных».

З цією метою згрупуємо вихідні дані наступним чином (табл. 7.7).

Таблиця 7.7

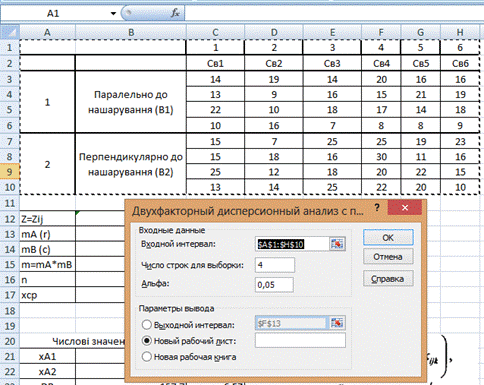
Потім активізуємо функцію «Двухфакторный дисперсионный анализ с повторениями» надбудови «Анализ данных» (рис. 7.1).

Для того щоб дана функція зробила вірні розрахунки потрібно для параметру «Входной интервал» виділити діапазон зі всією таблицею як показано на рис. 7.1.

Для параметру «Число строк для выборки» задати 4 (кількість рядків зі значеннями проникності для конкретної свердловини, що визначено в одному напрямку).

Для параметру «Альфа» потрібно ввести рівень істотності, який необхідний для оцінювання критичних параметрів F-статистики. В цьому випадку рівень істотності задано для розрахунків 0,05.

Результати розрахунків для вихідних даних прикладу наведено у таблиці 7.8 та 7.9. Пояснення до таблиці 7.9 наведено на рис. 7.2.

19. Виконуємо інтерпретацію отриманих даних. З цією метою будуємо графік середніх значень, які відповідають рівням факторів (рис. 7.3).

Рис. 7.1. Приклад використання функції «Двухфакторный дисперсионный анализ с повторениями» надбудови «Анализ данных»

Таблиця 7.8