
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Перевірка значимості коефіцієнтів регресіїПеревірка значимості коефіцієнтів рівняння регресії проводиться по t-критерію Ст’юдента. Гіпотеза про значимість коефіцієнтів регресії приймається, якщо виконується наступна нерівність:
де S0, Si, Sii, Sij, Sb0 – оцінка дисперсій коефіцієнтів рівняння регресії. Оцінка дисперсії коефіцієнтів рівняння регресії визначаються наступними виразами:
де S2 – оцінка дисперсії відтворюваності експерименту. Критичне значення критерію Ст’юдента tкр знаходять з таблиці розподілення Ст’юдента по числу степенів свободи та рівня значимості а (додаток В). Число степенів свободи f=N(k-l). Якщо нерівність 7.1 не виконується, коефіцієнт регресії вважається не значним і прирівнюється до нуля. Оскільки всі коефіцієнти оцінюються незалежно, то зміни оцінки будь-якого коефіцієнту (наприклад, виключення відповідного коефіцієнту з рівняння) не призведуть до змін інших оцінок та їх дисперсій. Виключення складають коефіцієнт b0, оскільки він пов'язаний з оцінками при квадратичних членах, тому їх виключення призводить до зміни b0. Необхідно пам’ятати, що не значимість коефіцієнтів може бути обумовлена і невірним вибором інтервалу варіювання. Тому іноді буває корисним розширити інтервал варіювання і провести новий експеримент. Перевірка адекватності отриманої математичної моделі Перевірка адекватності отриманого рівняння регресії експериментальними даними проводяться за допомогою критерію Фішера, розрахункове значення якого наступне відношення:
де S2ад – оцінка дисперсії неадекватності; S2y – оцінка дисперсії відтворюваності експерименту. Оцінка дисперсії неадекватності визначається за наступною формулою: 
де В – число значимих коефіцієнтів рівняння регресії; yjp – розрахункове значення функції реакції;
Якщо Fрасч<Fкрит, то гіпотеза про адекватність математичної моделі приймається. Критичне значення критерію Фішера Fкрит знаходиться з таблиці розподілу Фішера (див. додаток С) за кількістю степенів для чисельника f=k(N-B), знаменник f=N(k-l) та рівня значимості а. Перехід до фізичної змінної Для запису математичної моделі в реальних фізичних величинах роблять зворотній перехід від стандартизованого масштабу до натурального. Це можливо зробити, використовуючи відношення (2.6). Після чого записують остаточний вид моделі. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 497. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

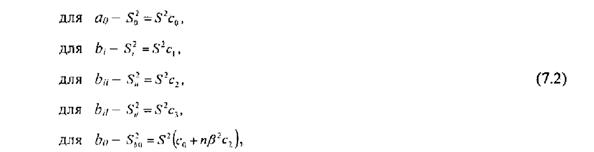
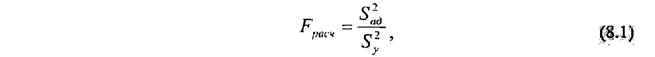

 - експериментальне значення функції реакції (див. табл. 3.1).
- експериментальне значення функції реакції (див. табл. 3.1).