
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Схема дисперсійного аналізу множинної лінійної регресії
У разі необхідності збільшення кількості факторів у рівнянні регресії проводять аналіз ефективності даної процедури, методика якої наведена у таблиці 10.2. Мета роботи:Дані значень коефіцієнта вилучення нафти η (табл. 10.3), динамічної в’язкості нафти μ (табл. 10.4), піщанистості пласта Kп (табл. 10.5), коефіцієнта проникності пласта k (табл. 10.6), об’ємного коефіцієнта нафти b (табл. 10.7) для десяти родовищ Дніпровсько-Донецької западини наведено у відповідних таблицях (згідно з варіантом студента). Необхідно знайти функціональну залежність коефіцієнта вилучення нафти η від динамічної в’язкості нафти μ, коефіцієнта піщанистості пласта Kп, коефіцієнта проникності пласта k, об’ємного коефіцієнта нафти b за допомогою множинної регресії.
Таблиця 10.2 Схема аналізу ефективності підвищення
Таблиця 10.3 Значення коефіцієнта вилучення нафти η
Таблиця 10.4 Значення динамічної в’язкості нафти μ, мПа·с
Таблиця 10.5 Значення коефіцієнта піщанистості пласта Kп
Таблиця 10.6 Значення коефіцієнта проникності пласта k, 10-3 мкм2
Таблиця 10.7 Значення об’ємного коефіцієнта нафти b
Хід роботи 1. У табл. 10.8 заносимо дані для свого варіанту. 2. Позначаємо X1=μ, X2=Кп, X3=lgk, X4=b, Y=η. Визначаємо lgk (функція «LOG10») і заносимо ці значення у стовпчик 7 табл. 10.8. Тоді рівняння множинної регресії буде мати наступний вигляд: Y=a0+a1Х1+a2Х2+a3Х3+a4Х4 η=a0+a1μ+a2Кп+a3lgk+a4b
Таблиця 10.8
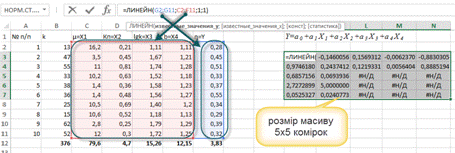
3. Для визначення коефіцієнтів регресії рекомендуємо використати функцію «ЛИНЕЙН» (рис. 10.1) чи «Регрессия» пакета «Анализ данных» (рис. 10.2). Для умов прикладу масив, який отримано за допомогою функції «ЛИНЕЙН», наведено у таблиці 10.9. Масив статистики у таблиці 10.9 розшифровується наступним чином:
де β0, β1, …, β4 коефіцієнти регресії; σ0, σ1, …, σ4 – стандартні значення похибок для коефіцієнтів регресії; R2 – процент врахування загальної мінливості (коефіцієнт детермінованості); σу – стандартне значення похибки для оцінювання у; F – критерій Фішера; df – ступінь свободи; ssreg – регресійна сума квадратів; ssresid – залишкова сума квадратів.
Рис. 10.1. Приклад використання функції «ЛИНЕЙН»
Для умов прикладу масив, який отримано за допомогою функції Регрессия» пакета «Анализ данных» наведено на рис. 10.3. 4. Для умов прикладу функція регресія буде мати наступний вигляд η=-0,88–0,01μ+0,16Кп–0,15lgk+1,21b. Коефіцієнт детермінації становить R2=0,69. Це означає, що знайдена математична модель контролює 69% мінливості коефіцієнта вилучення нафти. За геологічним змістом знайдене рівняння регресії дає можливість виконувати прогнозування коефіцієнта вилучення нафти при підготовці матеріалів для підрахунку запасів нафти та складанні технологічної схеми або проекту розробки родовищ.
Рис. 10.2. Приклад використання функції «Регрессия» пакета «Анализ данных» для підбору коефіцієнтів регресійного рівняння Таблиця 10.9
Рис. 10.3. Результати підбору коефіцієнтів регресійного рівняння за допомогою функції «Регрессия» пакета «Анализ данных»
Практичне заняття №11 Планування експериментальних досліджень
Мета роботи: отримати математичну модель технологічного процесу видобування нафти у вигляді рівняння множинної регресії другого порядку. Ортогональний центральний композитний план Розробка математичної моделі передбачає принцип «від простого до більш складного». В імітаційній моделі у вигляді поліному цей принцип передбачає перехід від поліному першого порядку
до поліному другого порядку
В цьому випадку, якщо за допомогою повного факторного експерименту не вдається отримати адекватну математичну модель, то переходять до центральних композиційних планів (ЦКП). Найбільшого поширення отримали ортогональний та рототабельний ЦКП. В ортогональному центральному композиційному плані (ОЦКП) до дослідів повного факторного експерименту (ПФЕ) або дробного факторного експерименту необхідно додати дослід у «зіркових точках» і дослід у центрі плану. Кількість дослідів ортогонального центрального композиційного плану визначається за наступною формулою:
де Nн – кількість дослідів у ядрі плану; n – кількість факторів. Ядром плану є повний факторний експеримент або дрібний факторний експеримент. Якщо число факторів n≤4, то ядром плану є повний факторний експеримент і кількість дослідів у ядрі плану дорівнює
Якщо кількість факторів n>4, то ядром плану є дрібний факторний експеримент і кількість дослідів у ядрі плану дорівнює
де р – кількість генераторів плану або кількість взаємодій, заміненими факоторами, які враховуються в експерименті. Важливою властивістю ЦКП є те, що інформація, яка була отримана при проведені повного факторного експерименту або дрібного факторного експерименту, не губиться, а використовується у наступних дослідженнях. 2n – це кількість дослідів у «зіркових точках», що мають координати: (±а, 0, 0,…, 0) (0, ±а, 0,…, 0) (0, 0, 0, …, ±а) де а – величина «зіркового плеча». У центрі плану – один дослід. Це точка факторного простору з координатами (0,0,0,…,0). Для зручності розрахунків і аналізу результатів переходять до нормативного масштабу факторів. Для і-го фактора
де хі – нормоване значення;
І – інтервал варіювання. Інтервал варіювання І дорівнює
У результаті нормування значення верхнього рівня фактору Складання матриці планування ОЦКП Для знаходження умов, що забезпечують ортогональність, квадратичну модель (11.2) можна записати у вигляді проміжної моделі
де Величина β вводиться для забезпечення ортогональності плану
Матрицю планування експерименту для двох факторів (п=2) можна представити у вигляді таблиці 11.1. В якості ядра плану використовують ПФЕ, оскільки п<4. Кількість дослідів ОЦКП буде рівним
Зіркове плече а можливо визначити за формулою
Значення величини а і β, які забезпечують ортогональність плану при різних значеннях п, наведені в таблиці 11.2. х0 – фіктивний параметр, відповідає коефіцієнту b0. Геометрична інтерпретація ортогонального ЦКП для двох факторів на рис. 11.1. і являє собою квадрат.
Матриця ОЦКП для двох факторів
Параметри ортогональних ЦКП
Рис. 11.1 Геометрична інтерпретація ОКЦ для двух факторів
Величина зіркового плеча а=1 для п=2. 9 – це дослід у центрі плану. Для п=3 геометричною інтерпретацією ПФЕ є куб, «зіркові точки» ОЦКП лежать за межами куба, оскільки вони розташовані на відстані більш ніж ±1 від центру плану, та лежать на поверхні сфери діаметром 2а (а=1,215). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 395. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



 ,
,



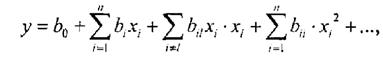
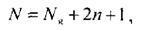
 .
. ,
, (11.3)
(11.3)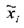 – натуральне значення;
– натуральне значення;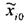 – основний рівень;
– основний рівень; (11.4)
(11.4)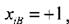 значення нижнього рівня фактору
значення нижнього рівня фактору  .
.








