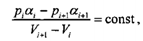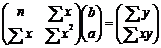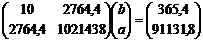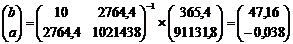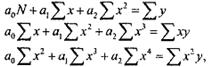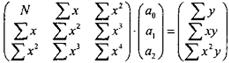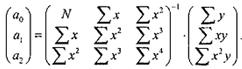Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Двофакторний дисперсійний аналіз з повтореннями
Таблиця 7.9 Дисперсійний аналіз
Рис. 7.2. Пояснення до таблиці 7.9
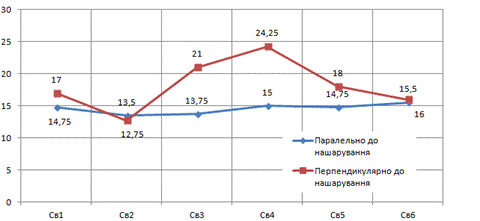
Рис. 7.3. Графік середніх значень коефіцієнта проникності (10-3 мкм2) керна залежно від напряму відбору проб та розміщення свердловин на родовищі
Таким чином, за аналітичним і графічним аналізом отримано, що просторова орієнтація має істотний вплив на проникність керна, особливо це спостерігається у свердловині №3 – №5.
Практичне заняття №8 Модель лінійної регресії
Теоретичні відомості за темою практичної роботи. Регресійний аналіз – статистичний аналіз вибіркових сукупностей з метою подання залежності однієї випадкової величини від декількох інших у вигляді математичних формул (графіків). Основні етапи регресійного аналізу: 1) вибір форми зв’язку та рівняння регресії; 2) обчислення коефіцієнтів вибраного рівняння; 3) оцінювання достовірності вибраного рівняння.  Основні критерії вибору рівняння регресії – метод найменших модулів і метод найменших квадратів. Метод найменших модулів – найкращою функцією регресії Y=f(x) вважається функція, для якої виконується умова мінімізації суми абсолютних величин відхилень вибіркових значень yі величини Y від значень функції f при значеннях хі величини Х. Метод найменших квадратів – найкращою функцією регресії Y=f(x) вважається функція, для якої виконується умова мінімізації суми квадратів відхилень вибіркових значень yі величини Y від значень функції f при значеннях хі величини Х. Найчастіше використовують наступні види рівнянь регресії: 1. Лінійні функції Y=ax+b та узагальнені лінійні функції 2. Поліноміальні функції 3. Логарифмічні функції 4. Показникові функції 5. Степеневі функції
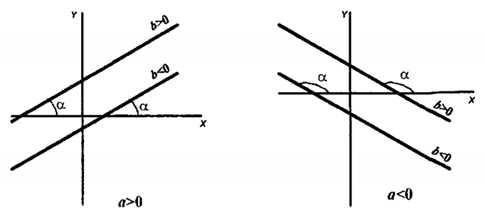
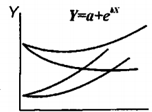
Рис. 8.1. Графіки лінійної залежності Y=ax+b при різних a і b Мета роботи:за даними гідродинамічних і геопромислових досліджень визначити початкові запаси газу у газовому покладі методом падіння тиску із використанням моделі простої лінійної регресії.
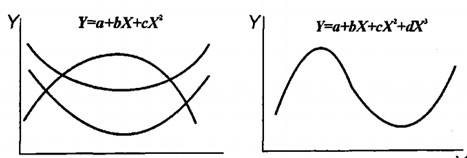
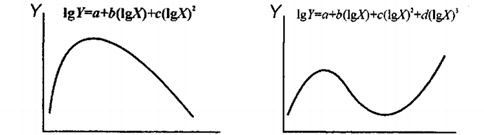
Рис. 8.2. Графіки поліноміальних функцій
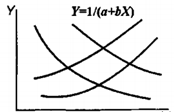
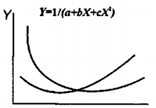
Рис. 8.3. Графіки обернених раціональних функцій
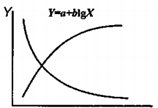
Рис. 8.4. Графіки показникових (зліва) та логарифмічних (справа) функцій
Рис. 8.5. Інші види нелінійних функцій Вихідні дані. Дано пластові тиски рпл (табл. 8.1), поправки на надстисливість газу α (табл. 8.2) та об’єми видобутого газу V (табл. 8.3), що наведено у відповідних таблицях залежно від варіанта студента. Для розв’язання цієї задачі потрібно використати той факт, що при газовому режимі покладу вилучення певного об’єму V газу з покладу супроводжується зниженням протягом усього періоду експлуатації покладу. Цей процес виражається наступним рівнянням:
де рі, рі+1 – значення пластового тиску на моменти часу і та і+1; ріαі= р0α0–сVі де р0 – значення початкового пластового тиску; α0 – поправка на надстисливість газу для тиску р0; Vі, Vі+1 – значення видобутого об’єму газу на моменти часу і та і+1. Початкові запаси газу V0 дорівнюють видобутому газу при ріαі=0,1. Тоді початкові запаси газу можна записати наступним рівнянням
Таблиця 8.1
Таблиця 8.2
Таблиця 8.3
Хід роботи 1. У табл. 8.4 (стовпчики 1–3) заносимо дані для свого варіанту. Далі робимо відповідні розрахунки і заповнюємо стовпчики 5–8. Таблиця 8.4
2. Позначимо: Х=V, Y=pα. Тоді рівняння регресії, яке нам потрібно скласти, буде мати наступний вигляд Y=ax+b, де невідомими параметрами будуть коефіцієнти a і b. Для того щоб їх знайти, потрібно скласти наступні матриці:
Для умов прикладу ці матриці набудуть наступного вигляду
3. Виконуємо розв’язання матричним методом. З цією метою рекомендується спочатку знайти обернену матрицю (функція «МОБР»), потім цю обернену матрицю потрібно помножити на матрицю відповідей (функція «МУМНОЖ»).
4. Тоді рівняння регресії буде мати наступний вигляд 5. Визначаємо коефіцієнт кореляції для даної залежності:
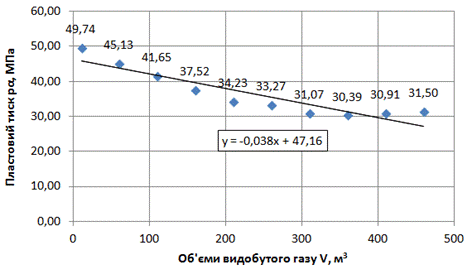
Коефіцієнт кореляції можна також знайти за допомогою функції «КОРРЕЛ» (для цього потрібно виділити першим масив об’єми видобутого газу, а другим – добуток пластового тиску і коефіцієнту надстисливості). Отриманий коефіцієнт кореляції становить |r|=0,96, що більше 0,7, а це означає високий кореляційний зв’язок між Y і Х. Таким чином, можна зробити висновок, що модель лінійної регресії добре підходить для оцінки падіння тиску в цьому газовому покладі при видобуванні газу і відповідно може бути використана для підрахунку початкових його запасів. 6. Для наочності проведених розрахунків зробимо наступну таблицю 8.5 та побудуємо графік (рис. 8.6). 7. Початкові запаси газу дорівнюють видобутому газу при ріαі=0,1 і складають V0=(0,1–47,16)/–0,038=1240 млн. м3.
Таблиця 8.5
Рис. 8.6. Графік фактичної залежності пластового тиску
Практичне заняття №9 Модель нелінійної регресії
Теоретичні відомості за темою практичної роботи. Для рівняння 2-го ступеня Y=a0+a1X+a2X2 система нормальних рівнянь має такий вигляд:
У матричній формі ця система нормальних рівнянь буде мати наступний вигляд:
Обчислення коефіцієнтів регресії зручно проводити матричним методом:
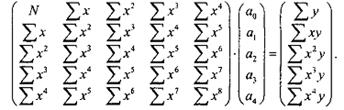
При збільшенні ступеня рівняння регресії підхід до визначення його коефіцієнтів залишається аналогічним. Наприклад для 4-го ступеня матриця буде мати наступний вигляд:
Для спрощення розрахунків нелінійні рівняння за рахунок перетворення змінних зводять до лінійних. Цей метод називається лінеаризацією. Схема дисперсійного аналізу нелінійної регресії наведено у таблиці 9.1.
Таблиця 9.1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 376. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

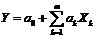 (рис. 8.1).
(рис. 8.1).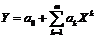 (рис. 8.2).
(рис. 8.2).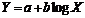 (рис. 8.4).
(рис. 8.4).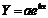 (рис. 8.4).
(рис. 8.4).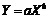 .
.