
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема6. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ.Классификация бесконечно малых функций. Определение 6.1.Пусть 1. Если 2. Если 3. Если 4. Если 5. Если данный предел не существует, то бесконечно малые функции Замечание 6.1.Аналогичным образом можно сравнивать бесконечно малые функции и при Некоторые эквивалентные бесконечно малые функциипри
Применение эквивалентных бесконечно малых функций. Для упрощения вычисления некоторых пределов можно использовать следующую теорему, основанную на эквивалентности бесконечно малых функций. Теорема 6.1.Пусть Примеры 6.1. Найти пределы, используя эквивалентные бесконечно малые: 1) Решение: В данном примере имеем дело с отношением двух бесконечно малых функций: числитель и знаменательстремятся к нулю при 
2) Решение: В данном примере также имеем дело с отношением двух бесконечно малых функций: числитель и знаменательстремятся к нулюпри
3) Решение: В данном примере снова имеем дело с отношением двух бесконечно малых функций: числитель и знаменательстремятся к нулюпри
Задания для самостоятельной работыпо теме «Эквивалентные бесконечно малые функции». Задание 1.Найти следующие пределы:
Тема7. НЕПРЕРЫВНОСТЬ ФУНЦИИ. |
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 269. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
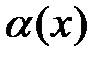 и
и  – бесконечно малые функции при
– бесконечно малые функции при  и известно, что
и известно, что  . Тогда
. Тогда , то бесконечно малые функции
, то бесконечно малые функции  и
и  называются эквивалентными при
называются эквивалентными при  и пишут
и пишут  при
при  .
. и
и  , то бесконечно малые функции
, то бесконечно малые функции  и
и  имеют одинаковый порядок малости.
имеют одинаковый порядок малости.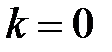 , то бесконечно малая функция
, то бесконечно малая функция  имеет более высокий порядок малости, чем функция
имеет более высокий порядок малости, чем функция  .
. , то бесконечно малая функция
, то бесконечно малая функция  имеет более высокий порядок малости, чем функция
имеет более высокий порядок малости, чем функция  .
. и
и 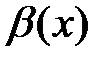 называются несравнимыми друг с другом при
называются несравнимыми друг с другом при  .
.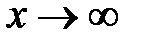 .
. :
: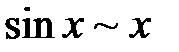

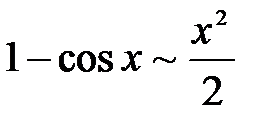


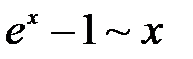
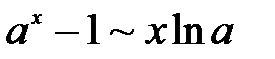


 и
и 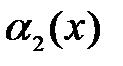 ,
,  и
и 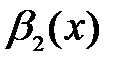 – попарно эквивалентные бесконечно малые функции при
– попарно эквивалентные бесконечно малые функции при  , т.е.
, т.е.  и
и 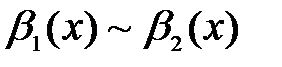 при
при  . Тогда если существует
. Тогда если существует  , то существует и
, то существует и 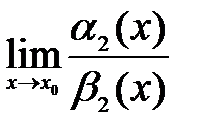 , при этом выполняется равенство
, при этом выполняется равенство  . Другими словами, предел отношения двух бесконечно малых функций не изменится, если их заменить эквивалентными бесконечно малыми функциями. Сказанное справедливо и для эквивалентных бесконечно малых функций при
. Другими словами, предел отношения двух бесконечно малых функций не изменится, если их заменить эквивалентными бесконечно малыми функциями. Сказанное справедливо и для эквивалентных бесконечно малых функций при  .
.  .
. . Поэтому для вычисления предела воспользуемся эквивалентностью бесконечно малых функций:
. Поэтому для вычисления предела воспользуемся эквивалентностью бесконечно малых функций:  и
и  при
при  . Тогда
. Тогда  .
. .
.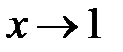 . Поэтомудля раскрытия неопределенности заменим числитель эквивалентной бесконечно малой функцией:
. Поэтомудля раскрытия неопределенности заменим числитель эквивалентной бесконечно малой функцией:  , а знаменатель разложим на множители:
, а знаменатель разложим на множители: .
. .
.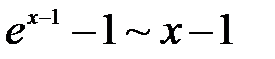 и далее воспользуемся формулой разности квадратов:
и далее воспользуемся формулой разности квадратов: 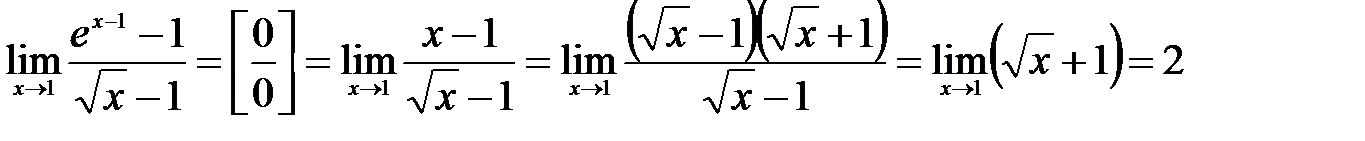 .
. .
.
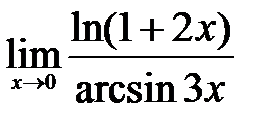 .
.
 .
.
 .
.
 .
.
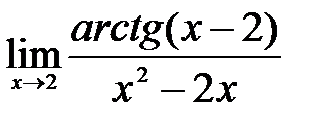 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.