
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Понятие непрерывности функции.Пусть функция Определение 7.1.Функция
Таким образом, данное равенство и само понятие непрерывности подразумевают выполнение трех следующих условий: 1) функция 2) существует предел функции 3) предел функции в точке Невыполнение хотя бы одного из этих условий означает то, что функция не является непрерывной в точке Определение 7.2. Пусть функция Определение 7.3.Разность соответствующих значений функции Используя введенные понятия приращения аргумента и приращения функции, дадим второе определение функции, непрерывной в точке. Определение 7.4.Функция
Используя ранее введенные понятия левостороннего и правостороннего пределов функции, дадим, наконец, третье определение функции, непрерывной в точке. Определение 7.5.Функция
Определение 7.6.Функция  Определение 7.7.Функция Пример 7.2.Доказать, что функция Решение: Докажем непрерывность данной функции по определению. Пусть
Тогда, применяя теоремы о пределе суммы и произведения функций, получим:
Таким образом, Пример 7.3.Доказать, что функция Решение: Докажем непрерывность данной функции снова по определению. Пусть
Тогда
В последнем равенстве воспользовались тем, что произведение ограниченной функции и бесконечно малой функции является бесконечно малой функцией.Таким образом, по определению (7.2), функция |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 228. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 определена в точке
определена в точке  и в некоторой окрестности этой точки.
и в некоторой окрестности этой точки. называется непрерывнойв точке
называется непрерывнойв точке  , если предел функции в этой точке равен значению функции в этой точке, т.е.
, если предел функции в этой точке равен значению функции в этой точке, т.е.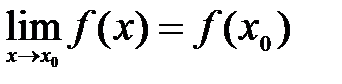 .
. определена в точке
определена в точке  и в окрестности этой точки;
и в окрестности этой точки; ;
; равен значению функции в этой точке.
равен значению функции в этой точке. определена в некотором интервале
определена в некотором интервале  и
и  – произвольная точка из этого интервала:
– произвольная точка из этого интервала: 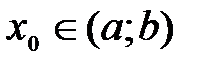 . Для любого
. Для любого  разность
разность  называется приращением аргумента
называется приращением аргумента  в точке
в точке 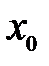 и обозначается
и обозначается  :
:  . Отсюда
. Отсюда  .
. называется приращением функции
называется приращением функции  в точке
в точке  и обозначается
и обозначается  (или
(или  или
или  ):
):  или
или  .
. называется непрерывнойв точке
называется непрерывнойв точке  , если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е.
, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е. .
.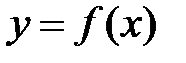 называется непрерывнойв точке
называется непрерывнойв точке  , если она определена в некоторой окрестности этой точки и выполняются следующие равенства:
, если она определена в некоторой окрестности этой точки и выполняются следующие равенства: .
. называется непрерывной в интервале
называется непрерывной в интервале  , если она непрерывна в каждой точке этого интервала.
, если она непрерывна в каждой точке этого интервала. называется непрерывной на отрезке
называется непрерывной на отрезке  , если она непрерывна в интервале
, если она непрерывна в интервале  и в точке
и в точке  непрерывна справа (т.е.
непрерывна справа (т.е.  ), а в точке
), а в точке  непрерывна справа (т.е.
непрерывна справа (т.е.  ).
). непрерывна в произвольной точке
непрерывна в произвольной точке  .
. – приращение аргумента в произвольной точке
– приращение аргумента в произвольной точке  . Вычислим соответствующее ему приращение функции:
. Вычислим соответствующее ему приращение функции:

 , а это и означает по определению, что функция
, а это и означает по определению, что функция 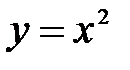 непрерывна в произвольной точке
непрерывна в произвольной точке  .
. непрерывна в произвольной точке
непрерывна в произвольной точке  .
. – приращение аргумента в произвольной точке
– приращение аргумента в произвольной точке  . Найдем соответствующее ему приращение функции:
. Найдем соответствующее ему приращение функции: .
. .
. непрерывна в произвольной точке
непрерывна в произвольной точке  множества
множества  .
.