Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Некоторые приемы раскрытия неопределенностей при вычислении пределов.Если подставить предельное значение аргумента в функцию, предел которой необходимо вычислить, то можно получить различные виды так называемых неопределенностей или неопределенных выражений: I. Если требуется вычислить предел отношения двух многочленов или комбинаций степенных функций при Примеры 4.4.Вычислить пределы: 1) Решение: В данном примере имеем дело с неопределенностью
В последних равенствах учли, что предел константы – константа, а функции 2) Решение: В данном примере также имеем дело с неопределенностью
В последнем равенстве также воспользовались соответствующей теоремой о бесконечно малых и бесконечно больших функциях. 3) Решение:Вначале для вычисления предела применим теорему о предельном переходе, а затем для того, чтобы раскрыть неопределенность 
В последних равенствах учли, что предел константы – константа, а функции II. Если требуется вычислить предел отношения двух многочленовпри Примеры 4.5.Вычислить пределы: 1) Решение: В данном примере имеем дело с неопределенностью
В последних равенствах воспользовались непрерывностью функции в точке (см. тему «Непрерывность функции.Точки разрыва»): для непрерывной функции 2) Решение: Аналогично решению предыдущего примера:
Пример 4.6.Вычислить предел Решение: Функция под знаком предела содержит иррациональности. Приведем ее к рациональному виду с помощью замены переменной.
III. Если требуется вычислить предел отношения двух функций, содержащих иррациональные выражения, то необходимо числитель и знаменатель домножить на выражение, сопряженное по отношению к иррациональному выражению, и затем воспользоваться формулой разности квадратов (или разности кубов). Примеры 4.7.Вычислить пределы: 1) Решение: В данном примере имеем дело с неопределенностью
2) Решение: В данном примере имеем дело с неопределенностью
В последнем равенстве также воспользовались соответствующей теоремой о бесконечно малых и бесконечно больших функциях. 3) Решение: В данном примере при
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 264. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
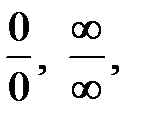
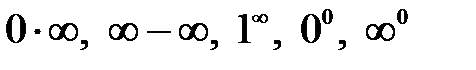 . Поэтому при вычислении пределов первоочередная задача – это раскрыть подобного рода неопределенности или, другими словами, избавиться от них. Рассмотрим некоторые приемы раскрытия основных типов неопределенностей.
. Поэтому при вычислении пределов первоочередная задача – это раскрыть подобного рода неопределенности или, другими словами, избавиться от них. Рассмотрим некоторые приемы раскрытия основных типов неопределенностей.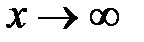 , то необходимо числитель и знаменатель этого отношения разделить на
, то необходимо числитель и знаменатель этого отношения разделить на 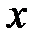 в старшей степени.
в старшей степени. .
.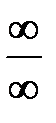 : числитель и знаменатель стремятся к бесконечности при
: числитель и знаменатель стремятся к бесконечности при 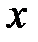 в старшей степени, т.е. на
в старшей степени, т.е. на 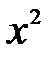 , и воспользуемся основными теоремами о пределах функции:
, и воспользуемся основными теоремами о пределах функции: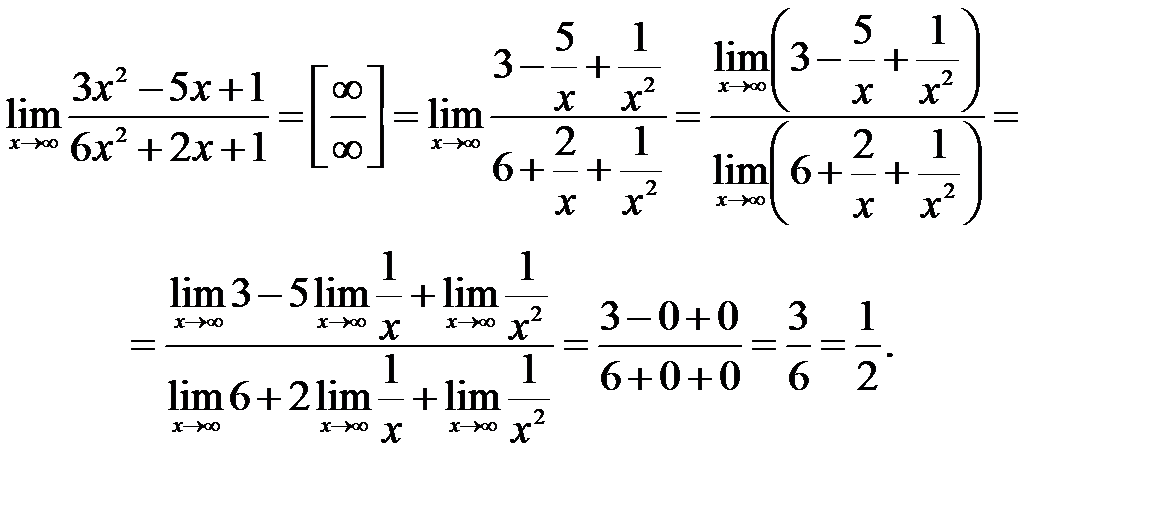
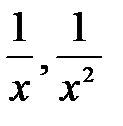 – бесконечно малые при
– бесконечно малые при 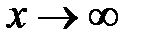 .
.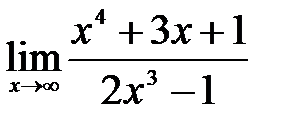 .
. , и воспользуемся далее основными теоремами о пределах функции:
, и воспользуемся далее основными теоремами о пределах функции: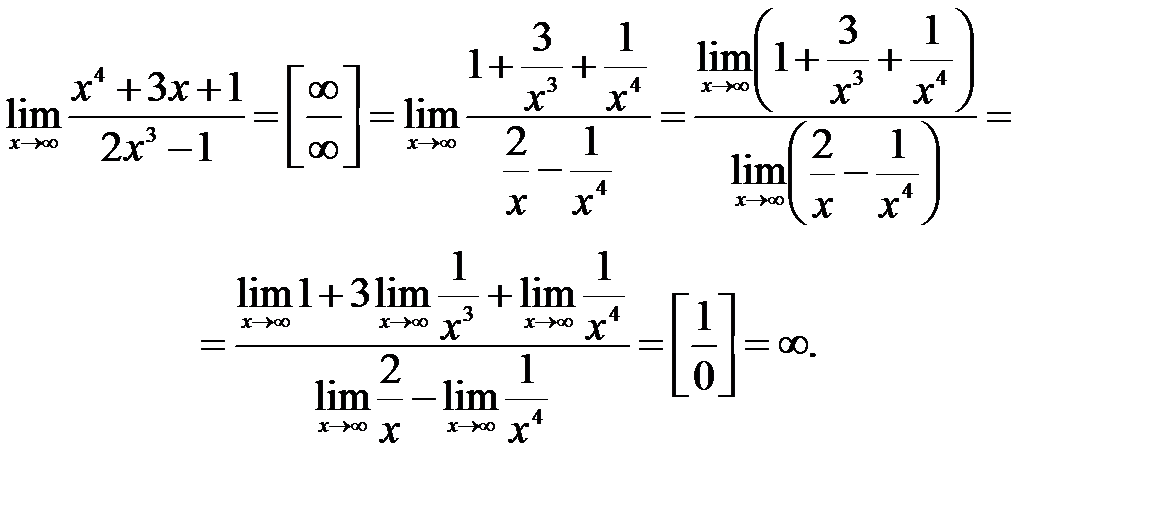
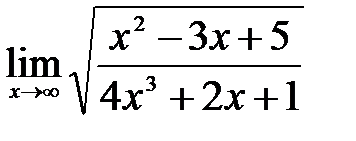 .
.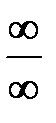 ,поделим числитель и знаменатель на
,поделим числитель и знаменатель на 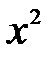 , после чего применим основные теоремы о пределах функции:
, после чего применим основные теоремы о пределах функции: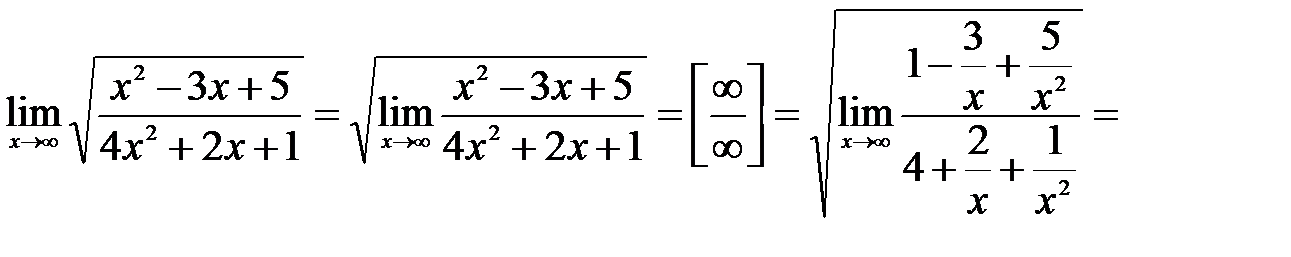
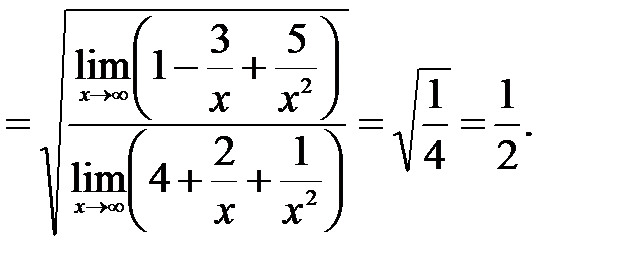
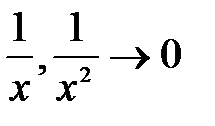 при
при 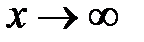 .
.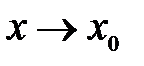 , каждый из которых стремится к нулю при этом же условии, то необходимо в числителе и знаменателе выделить множитель
, каждый из которых стремится к нулю при этом же условии, то необходимо в числителе и знаменателе выделить множитель 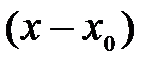 и затем сократить дробь на данный множитель.
и затем сократить дробь на данный множитель.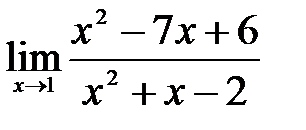 .
.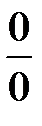 : числитель и знаменатель стремятся к нулю при
: числитель и знаменатель стремятся к нулю при 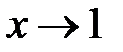 . Дляее раскрытия разобъем многочлены в числителе и знаменателе на множители и далее сократим их на общий множитель
. Дляее раскрытия разобъем многочлены в числителе и знаменателе на множители и далее сократим их на общий множитель 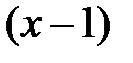 :
: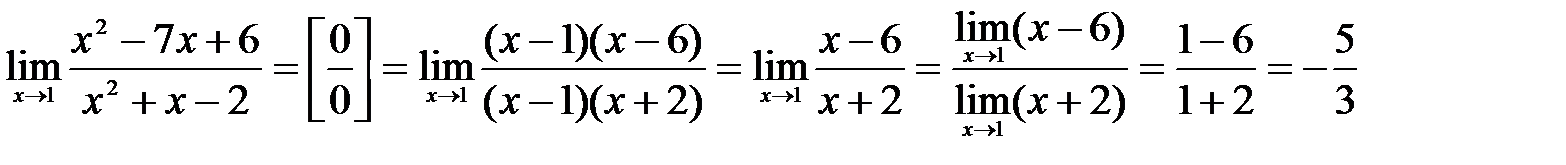 .
.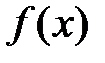 в точке
в точке 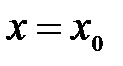 выполняется равенство
выполняется равенство  .
.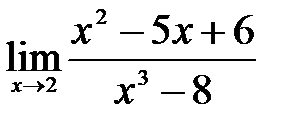 .
.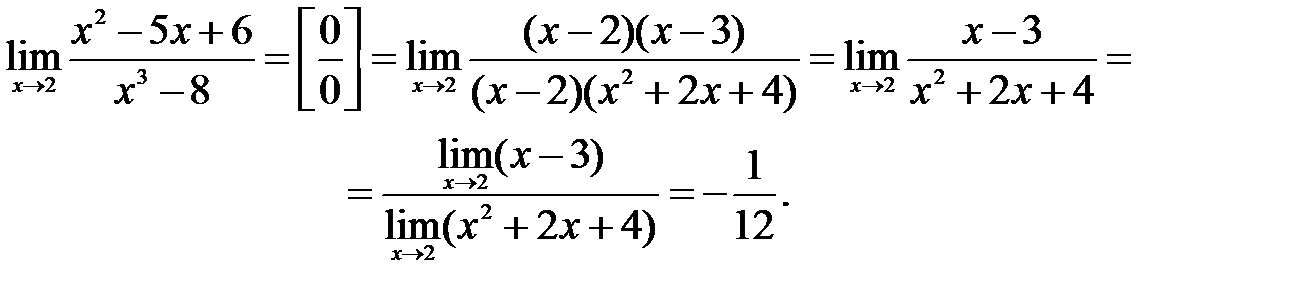
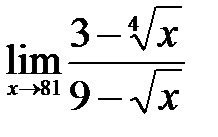 .
.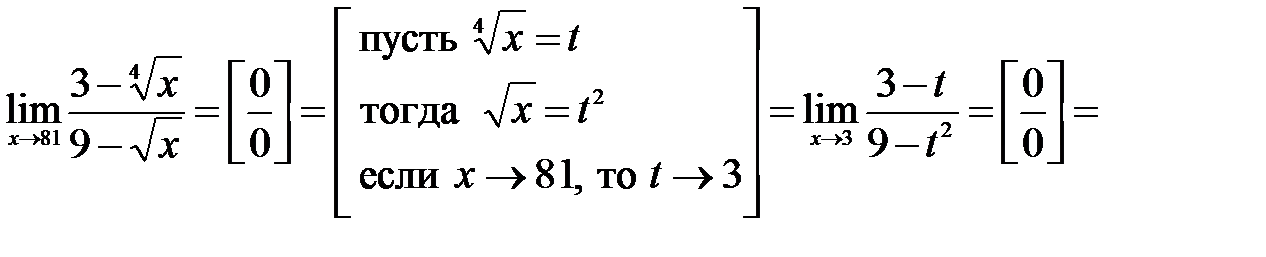

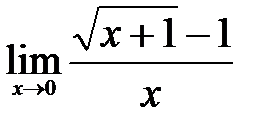 .
.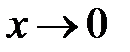 .Для ее раскрытия домножим числитель и знаменатель на выражение
.Для ее раскрытия домножим числитель и знаменатель на выражение  , которое является сопряженнымпо отношению к числителю, тем самым дополним числитель до формулы разности квадратов:
, которое является сопряженнымпо отношению к числителю, тем самым дополним числитель до формулы разности квадратов: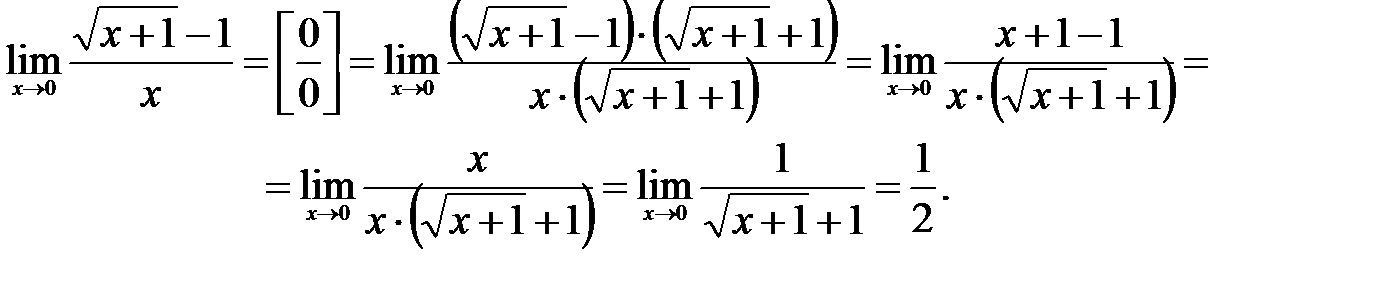
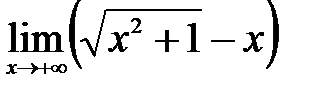 .
.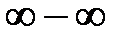 : первое и второе слагаемые стремятся к бесконечности при
: первое и второе слагаемые стремятся к бесконечности при 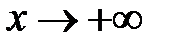 .Для ее раскрытия умножим и поделим выражениепод пределом на
.Для ее раскрытия умножим и поделим выражениепод пределом на 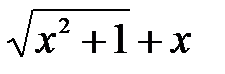 , после чего воспользуемся формулой разности квадратов:
, после чего воспользуемся формулой разности квадратов: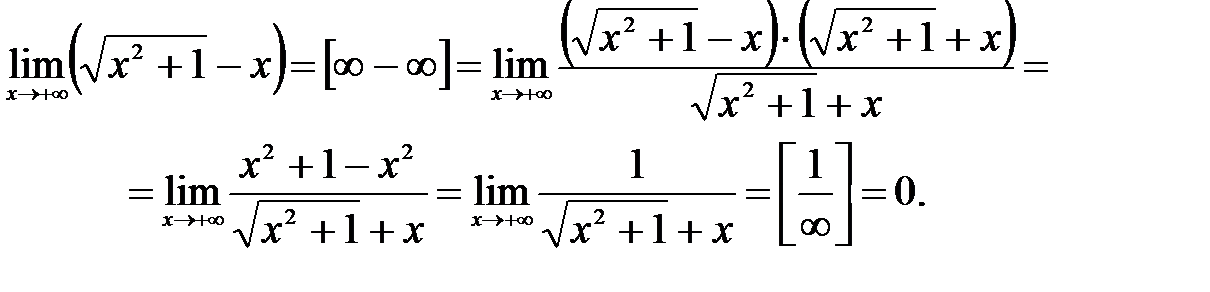
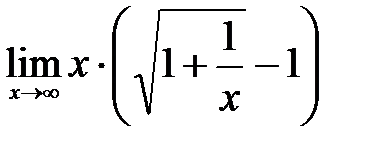 .
.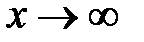 приходим к неопределенности
приходим к неопределенности  . Для ее раскрытия также умножим и поделим выражение под пределом на сопряженное по отношению к нему выражение, и снова воспользуемся формулой разности квадратов:
. Для ее раскрытия также умножим и поделим выражение под пределом на сопряженное по отношению к нему выражение, и снова воспользуемся формулой разности квадратов: