
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Бесконечно малые и бесконечно большие числовые последовательности.Определение 3.7.Числовая последовательность Пример 3.2.Примеры бесконечно малыхчисловых последовательностей: а) Определение 3.8.Числовая последовательность Пример 3.3.Примеры бесконечно большихчисловых последовательностей: а) Основные свойства предела числовой последовательности. 1. Если числовая последовательность имеет предел, то он единственный. 2. Если числовая последовательность имеет предел, то она ограничена. 3. Если числовая последовательность является монотонной и ограниченной, то она имеет предел. 4. Постоянная числовая последовательность, члены которой равны 5. Пусть общие члены трехчисловых последовательностей 6. Для того чтобы числовая последовательность Операции над пределами числовых последовательностей. 1. Предел суммы (разности) двух сходящихся числовых последовательностей равен сумме (разности) их пределов:
2. Предел произведения двух сходящихся числовых последовательностей равен произведению их пределов:
В частности: – постоянный множитель можно выносить за знак предела:
– предел натуральной степени от сходящейся последовательности равен этой степени от ее предела:
3. Предел частного двух сходящихся числовых последовательностей равен частному их пределов: 
4. Предел корня
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 217. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 называется бесконечно малой, если
называется бесконечно малой, если  .
. ; б)
; б)  .
. называется бесконечно большой, если
называется бесконечно большой, если  , то есть, другими словами, если для любого положительного числа
, то есть, другими словами, если для любого положительного числа  найдется такое натуральное число
найдется такое натуральное число  , что для всех
, что для всех  выполняется неравенство
выполняется неравенство  .
.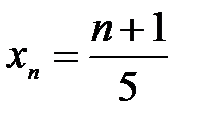 ; б)
; б)  .
. , сходится к этому числу:
, сходится к этому числу:  .
.  ,
,  и
и  удовлетворяют условию
удовлетворяют условию  ,
,  . Тогда если
. Тогда если  и
и  , то
, то  .
. имела предел
имела предел  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы  , где
, где  – бесконечно малая последовательность (
– бесконечно малая последовательность (  ).
). .
. .
. ;
;

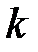 -й степени от сходящейся числовой последовательности равен корню этой же степени от предела числовой последовательности:
-й степени от сходящейся числовой последовательности равен корню этой же степени от предела числовой последовательности: