Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Закон инерции квадратичных форм
ПРИМЕР: Квадратичная форма:
двумя различными способами приведена к следующим каноническим видам:
Сравнение этих канонических видов одной и той же квадратичной формы показывает, что в обоих видах число положительных слагаемых равно 2, а отрицательных – 1.
Квадратичная форма L называется положительно (отрицательно) определенной, если при любых значениях переменных, из которых хотя бы одно отлично от нуля, выполняется неравенство L > 0 (L < 0).
Существуют различные критерии для установления знаковой определенности квадратичных форм. Приведем два из них как наиболее употребительные.
Критерий Сильвестра
В критерии Сильвестра под главными минорами матрицы понимают миноры i – го порядка, построенные следующим образом:
ПРИМЕР: Покажите положительную определенность квадратичной формы: Найдем вначале матрицу этой формы. Поскольку эту форму можно переписать в виде:
Характеристическое уравнение для этой матрицы будет иметь вид:
 Решая его, найдем:
Теперь найдем главные миноры матрицы А:
Поскольку оба полученных минора положительны, на основании критерия Сильвестра заключаем, что данная квадратичная форма является положительно определенной.
Рекомендуемая литература по Теме 3:[1 ÷ 3]. ВОПРОСЫ для самопроверке знаний по теме 3: 1. При каком значении с векторы
2. Сколько векторов будет содержать базис пространства
3. Можно ли образовать ортонормированный базис из двух векторов:
4. В какие векторы преобразует векторы (1, 0) и (0, 1) линейный оператор, заданный матрицей
5. Является ли число 1 собственным значением матрицы
6. Будет ли положительно определенной квадратичная форма
Тема 4. Элементы аналитической геометрии в пространстве После выбора системы координат Oxyz в трехмерном евклидовом пространстве точки и векторы этого пространства становятся тройками чисел: A(x, y, z),
Уравнения плоскости Пусть заданы: прямоугольная система координат Oxyz; произвольная плоскость p; точка
Рис. 4.1.
Рассмотрим на плоскости p произвольную точку
это условие можно записать в виде:
Это уравнение и есть уравнение плоскости, проходящей через точку М0 перпендикулярно вектору
Если в последнем уравнении раскрыть скобки и ввести обозначение:
При этом вектор
Очевидно, что угол j между плоскостями, заданными общими уравнениями:
будет определяться углом j между нормальными векторами:
Условие параллельности рассматриваемых плоскостей эквивалентно условию коллинеарности нормальных векторов этих плоскостей, т.е. может быть записано в виде:
В свою очередь, условие перпендикулярности плоскостей вытекает из условия перпендикулярности нормальных векторов, т.е. из равенства нулю их скалярного произведения, и может быть записано в виде:
|
||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 297. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 .
.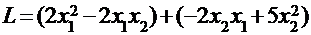 , искомая матрица имеет вид:
, искомая матрица имеет вид:
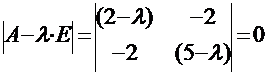 , или:
, или:  .
. , следовательно, на основании первого критерия можно заключить, что данная квадратичная форма является положительно определенной.
, следовательно, на основании первого критерия можно заключить, что данная квадратичная форма является положительно определенной. .
. и
и  будут перпендикулярны?
будут перпендикулярны? ?
? ?
? ?
? ?
? ?
?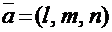 . После такой замены геометрические свойства фигур можно изучать методами алгебры и анализа, т.е. методами аналитической геометрии. Ниже рассмотрены только простейшие фигуры и их основные свойства.
. После такой замены геометрические свойства фигур можно изучать методами алгебры и анализа, т.е. методами аналитической геометрии. Ниже рассмотрены только простейшие фигуры и их основные свойства.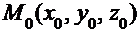 , лежащая на плоскости p; а также вектор
, лежащая на плоскости p; а также вектор  , перпендикулярный плоскости p (рис. 4.1).
, перпендикулярный плоскости p (рис. 4.1).
 . Очевидно, что эта точка будет лежать на плоскости p тогда и только тогда, когда векторы
. Очевидно, что эта точка будет лежать на плоскости p тогда и только тогда, когда векторы  и
и  будут взаимно перпендикулярны (ортогональны), т.е. когда их скалярное произведение будет равно нулю. Поскольку:
будут взаимно перпендикулярны (ортогональны), т.е. когда их скалярное произведение будет равно нулю. Поскольку: и
и 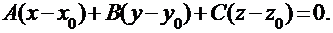
 , то получим общее уравнение плоскости:
, то получим общее уравнение плоскости:
 и
и 
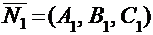 и
и  этих плоскостей, а косинус этого угла может быть найден по формуле:
этих плоскостей, а косинус этого угла может быть найден по формуле: