Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Квадратичные формы и их свойстваКвадратичной формой
Коэффициенты квадратичной формы
ПРИМЕР: Найдите матрицу квадратичной формы, записанной в виде: Поскольку искомая матрица должна быть симметрической, то она должна содержать в качестве элементов главной диагонали коэффициенты при квадратах переменных, а в качестве остальных элементов – половины коэффициентов при произведениях переменных. Поэтому перепишем квадратичную форму в виде:
Расставив коэффициенты в круглых скобках в соответствующие строки матрицы, получим матрицу заданной квадратичной формы в виде:
Если ввести в рассмотрение две матрицы: ХТ – матрицу-строку переменных и Х – матрицу-столбец переменных, то любую квадратичную форму можно записать в матричном виде:
Можно показать, что при невырожденном линейном преобразовании переменных
При некоторых удачно выбранных линейных преобразованиях переменных вид квадратичной формы можно существенно упростить, приведя матрицу этой формы к диагональному виду.
Квадратичная форма L называется канонической, или имеющей канонический вид, если ее матрица является диагональной, т.е. 
Для приведения квадратичной формы к каноническому виду используются разнообразные методы, среди которых наиболее часто применяется метод выделения полных квадратов. Покажем работу этого метода на конкретном примере.
ПРИМЕР:Привести к каноническому виду квадратичную форму, имеющую вид: Выделим полный квадрат при переменной
Таким образом, невырожденное линейное преобразование переменных:
Полученные различными методами канонические виды одной и той же квадратичной формы в самом общем случае различаются значениями коэффициентов при новых переменных. Однако эти канонические виды обладают важным свойством:
|
||||
|
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 245. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
от n переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторыми числовыми коэффициентами:
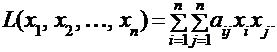
являются любыми действительными числами, причем 
. Матрица А, составленная из этих коэффициентов, называется матрицей квадратичной формы. Матрица А всегда имеет симметричный относительно главной диагонали вид и поэтому часто называется симметрической.
.
, т.е. при переходе от переменных xi к переменным yi , матрица квадратичной формы изменится и примет вид: 
.
.
, т.е. перепишем заданную квадратичную форму в виде:
позволило привести данную квадратичную форму к каноническому виду: 
.