Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Размерность и базис векторного пространстваВектор
Векторы
В противном случае, т.е. когда это тождество выполняется только при
Линейное векторное пространство R называется n-мерным, если в нем существует n линейно независимых векторов, а любые из (n + 1) векторов уже являются линейно зависимыми.
Совокупность n линейно независимых векторов n-мерного линейного векторного пространства R называется его базисом.
Можно доказать следующее утверждение:
ПРИМЕР: Если в n-мерном векторном пространстве R задан базис
Замечание. Каждый вектор однозначно определяется координатами в некотором базисе. При этом нулевой вектор имеет в этом базисе нулевые координаты, а противоположный данному вектор – противоположные по знаку координаты.
Если имеется система n линейно независимых векторов пространства R и любой вектор этого пространства линейно выражается через векторы этой системы, то пространство R является n-мерным, а указанная система векторов – его базисом. 
ПРИМЕР: Даны векторы Данные векторы образуют базис, если они являются линейно независимыми. Поэтому запишем для них тождество (*) сразу в матричном виде:
Этому тождеству соответствует система линейных однородных уравнений вида:
Поскольку определитель матрицы этой системы отличен от нуля |А| = 7 ≠ 0, согласно правилу Крамера, система имеет единственное нулевое решение: λ1 = λ2 = λ3 = 0. Это и означает, что заданные векторы – линейно независимы и образуют базис.
Переход к новому базису Пусть в пространстве R имеется два базиса: «старый»
Это же представление можно записать в матричной форме:
Полученная запись означает, что переход от старого базиса к новому задается матрицей перехода А. Эта матрица, как и матрица АТ невырожденная, т.к. в противном случае ее строки (а, следовательно, и базисные векторы) оказались бы линейно зависимы. Найдем зависимость между координатами одного и того же вектора в разных базисах. Пусть некоторый вектор
Если теперь подставить в среднюю часть этих равенств выражения для векторов
Систему представлений (**) можно записать и в матричной форме, т.е. в виде: Х = А∙Х*,именно так координаты вектора в старом базисе выражаются через координаты того же вектора в новом базисе. Если решить систему уравнений (**) методом обратной матрицы (это можно сделать, т.к. матрица A невырожденная, и обратная ей матрица существует), то получим: Х* = А-1Х именно таким образом координаты вектора в новом базисе выражаются через координаты того же вектора в старом базисе.
ПРИМЕР:Найдите координаты вектора Используя разложения векторов
Можно убедиться в том, что определитель этой матрицы |А| = 7 ≠ 0. Поэтому существует обратная ей матрица, которая имеет вид (убедитесь в этом самостоятельно):
Для отыскания координат вектора
Таким образом разложение вектора по векторам нового базиса можно записать в виде:
Евклидово пространство Выше мы ввели понятие линейного векторного пространства, в котором определены операции сложения векторов и умножения их на число, а также ввели понятия размерности и базиса этого пространства. Теперь дополним это пространство метрикой, т.е. укажем способы измерения длин векторов и углов между ними. Это можно сделать, доопределив в векторном пространстве понятие скалярного произведения векторов, естественно, обобщив его на случай n-мерных векторов.
Определение. Скалярным произведением двух векторов
Отметим основные свойства скалярного произведения, которые непосредственно вытекают из сформулированного определения.
1. 2. 3. 4.
Определение.Линейное векторное пространство, в котором определено скалярное произведение векторов, удовлетворяющее указанным четырем свойствам, рассматриваемым как аксиомы, называется евклидовым пространством.
Определение. Длинойили нормойвектора
Определенная таким образом норма вектора обладает некоторыми свойствами, основное из которых записывается в виде: Очевидно, что косинус угла j между двумя векторами
Определение.Два вектора называются ортогональными, если их скалярное произведение равно нулю.
Определение.Векторы
Существует теорема, устанавливающая одно из основных свойств евклидова пространства.
Примером одного из таких ортонормированных базисов является система из n единичных векторов, у которых i-ая компонента равна 1, а все остальные компоненты равны нулю, т.е. базис из векторов:
Линейные операторы Если задан закон (правило), по которому каждому вектору Оператор
· ·
Опираясь на свойства линейности оператора, можно показать, что его воздействие на вектор При переходе к другому базису в пространстве Rn матрица линейного оператора изменится. Можно показать, что матрицы А* и А линейного оператора
Определение. Ненулевой вектор
Из приведенного определения следует, что собственный вектор под воздействием линейного оператора переходит в вектор, коллинеарный самому себе, т.е. просто умножается на число – собственное значение, ему соответствующее.
Характеристическим уравнением матрицы А линейного оператора называется уравнение:
где λ – неизвестное собственное значение, Е – единичная матрица.
ПРИМЕР: Для матрицы
характеристическое уравнение будет иметь вид:
Таким образом, задача отыскания собственных векторов и собственных значений линейного оператора решается в следующей последовательности. Вначале составляют и решают характеристическое уравнение. Его решениями будут собственные значения, причем их количество не превосходит n. После этого, подставляя последовательно каждое из найденных собственных значений в систему однородных уравнений вида:
каждый раз решают ее методом Гаусса и выясняют структуру нетривиальных решений – координат собственного вектора, соответствующего данному собственному значению.
ПРИМЕР: Найдите собственные векторы линейного оператора, заданного матрицей:
Составим характеристическое уравнение для отыскания собственных значений:
Решениями этого уравнения будут два собственных значения преобразования А: λ1 = 2 и λ2 = − 1. Приступим к отысканию собственного вектора, соответствующего первому из собственных значений. Для этого запишем систему однородных уравнений:
Полученная система фактически представляет собой одно уравнение с двумя неизвестными. Положим
где С1 – любое действительное число, отличное от нуля. Для второго собственного значения система однородных уравнений запишется в виде:
Т.е. представляет собой одно уравнение с двумя неизвестными. Полагая
где С2 – любое действительное число, отличное от нуля.
|
|||||
|
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 331. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
называется линейной комбинацией векторов 
векторного пространства, если он равен сумме произведений этих векторов на произвольные действительные числа 
, т.е.:
векторного пространства называются линейно зависимыми, если существуют такие числа 
, не равные нулю одновременно, что выполняется тождество:
. (*)
для всех 
векторы 
, то любой вектор 
этого пространства может быть представлен в виде разложения по векторам этого базиса: 
. При этом числа 
называются координатами вектора 
, где векторы 
образуют базис линейного трехмерного пространства. Покажите, что данные векторы также являются базисом этого пространства.
и «новый» 
. Очевидно, что каждый из векторов нового базиса можно представить в виде линейной комбинации векторов старого базиса:
(*)
относительно старого базиса и координаты 
относительно нового базиса, т.е. можно записать:
из равенств (*), то после несложных преобразований можно получить: 
(**)
в новом базисе 
примера подраздела 3.3.
.
в новом базисе 
и 
называется число, равное:
- коммутативное свойство;
- дистрибутивное свойство;
- свойство справедливое для любого действительного α;
, если 
, и 
, если 
.
и носит название неравенства Коши-Буняковского.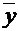
можно определить равенством, непосредственно вытекающим из неравенства Коши-Буняковского:
, где: 
и т.д.
и записывают 
.
- свойство аддитивности оператора;
- свойство однородности оператора.
, где С – матрица перехода от старого базиса к новому (см. подраздел 3.4).
. При этом число λ называется собственным значением оператора 
.
и найдем 
. Таким образом, собственный вектор, соответствующий первому из собственных значений, будет иметь следующие координаты:
,
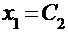, найдем 
, и окончательно запишем:
,