
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Прохождение СП через линейные системыВыражение (5.1), устанавливающее взаимосвязь входного и выходного СП позволяет оценить характеристики СП на выходе линейной системы. В частности, математическое ожидание выходного СП равно:
а его корреляционная функция определяется выражением вида:
или же
Дисперсия СП на выходе линейной системы связана с корреляционной функцией простым соотношением:
Взаимная корреляционная функция СП на входе и выходе линейной системы может быть определена по аналогии с корреляционной функцией в виде:
или же
Важными с практической точки зрения являются случаи дифференцирования и интегрирования СП. Рассмотрим их по очереди. Дифференцирование СП При дифференцировании СП, как и любого детерминированного сигнала, операторное изображение сигнала
Таким образом, операторная функция системы равна:
Операторная функция представляет собой изображение импульсной характеристики системы и в соответствии с теоремой дифференцирования может быть представлена через δ-функцию в виде:
Тогда математическое ожидание СП на выходе дифференцирующей цепи будет равно:
где штрих обозначает производную по времени. Таким образом, математическое ожидание СП на выходе дифференцирующей цепи равно производной от математического ожидания СП на входе этой цепи. А, значит, если СП на входе дифференцирующей цепи является стационарным, то СП на выходе этой цепи будет также стационарным. Иначе говоря, дифференцирующая цепь не нарушает стационарности СП.  Корреляционная функция СП на выходе дифференцирующей цепи может быть найдена подстановкой (5.10) в (5.7). Действительно:
Повторная подстановка дает:
Таким образом:
Тогда дисперсия СП на выходе дифференцирующей цепи равна:
Аналогично, подстановка (5.10) в (5.9) позволяет получить выражение для взаимной корреляционной функции СП на входе и выходе дифференцирующей цепи:
Таким образом:
Для случая стационарного СП на входе дифференцирующей цепи корреляционная функция СП на выходе цепи может быть найдена следующим образом:
где двойной штрих обозначает вторую производную по времени. Тогда дисперсия СП на выходе дифференцирующей цепи равна:
Аналогично, выражение для взаимной корреляционной функции СП на входе и выходе дифференцирующей цепи принимает вид:
где штрих обозначает производную. На практике узкополосные СП часто имеют корреляционную функцию одного из двух видов: а) с огибающей вида
В первом случае выражение (3.16) дает:
а во втором случае:
Интегрирование СП При интегрировании СП, как и любого детерминированного сигнала, операторное изображение сигнала
Таким образом, операторная функция системы равна:
Операторная функция представляет собой изображение импульсной характеристики системы и таким образом равна:
Тогда математическое ожидание СП на выходе интегрирующей цепи будет равно:
и даже если СП на входе интегрирующей цепи является стационарным и
Единственное исключение из данного правила составляет случай, когда математическое ожидание СП на входе интегрирующей цепи равно нулю. Тогда Корреляционная функция СП на выходе интегрирующей цепи принимает вид:
и даже если СП на входе интегрирующей цепи стационарный и Тогда дисперсия СП на выходе интегрирующей цепи равна:
И, наконец, взаимная корреляционная функция СП на входе и выходе интегрирующей цепи равна:
Лабораторное задание |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 201. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (5.6)
, (5.6)

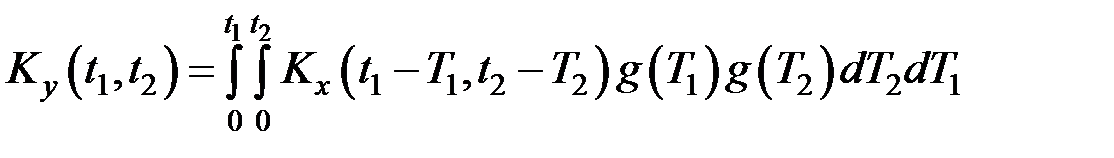 . (5.7)
. (5.7) . (5.8)
. (5.8)
 . (5.9)
. (5.9) умножается на оператор Лапласа
умножается на оператор Лапласа  , то есть:
, то есть: .
. .
. . (5.10)
. (5.10) (5.11)
(5.11)


 . (5.12)
. (5.12)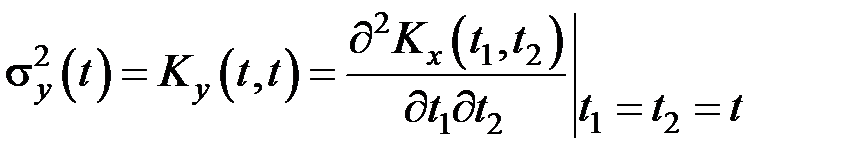 . (5.13)
. (5.13)

 . (5.14)
. (5.14) , (5.15)
, (5.15)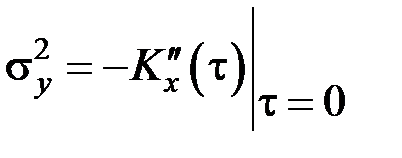 . (5.16)
. (5.16)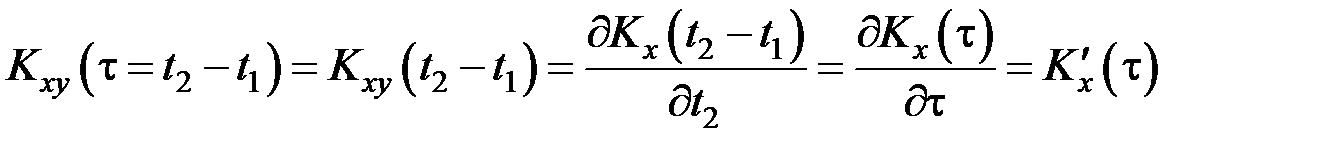 , (5.17)
, (5.17) и
и  ,
,  .
. , (5.18а)
, (5.18а) . (5.18б)
. (5.18б)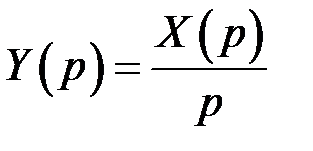 .
. .
.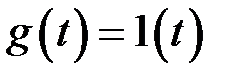 . (5.19)
. (5.19) (5.20)
(5.20) , СП на выходе этой цепи будет нестационарным:
, СП на выходе этой цепи будет нестационарным: . (5.21)
. (5.21) и сделать заключение о нестационарности СП по математическому ожиданию не оказывается возможным. Таким образом, в общем случае, интегрирующая цепь нарушает стационарность СП.
и сделать заключение о нестационарности СП по математическому ожиданию не оказывается возможным. Таким образом, в общем случае, интегрирующая цепь нарушает стационарность СП. (5.22)
(5.22) значение интегралов зависят непосредственно от
значение интегралов зависят непосредственно от  и
и  , а, значит, СП на выходе интегрирующей цепи является нестационарным.
, а, значит, СП на выходе интегрирующей цепи является нестационарным. . (5.23)
. (5.23) . (5.24)
. (5.24)