
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Разложение функций в степенные ряды.Ряды Тейлора, Маклорена
Пусть дана функция
Задача состоит в определении коэффициентов
Полагая в этих равенствах
Тогда Подставляя значения найденных коэффициентов
или
Это разложение функции Рядом Тейлора называю ряд вида:
или
называют разложением по степеням
Пример 45 Разложить в ряд Маклорена функцию Решение: Найдем производные
Этот ряд сходится на всей числовой прямой
Пример 46 Разложить в ряд Маклорена функцию Решение:
Так как производная четвертого порядка совпадает с функцией, то производные следующих порядков повторяются в той же последовательности. Найдем значения функции и ее производных при
Поэтому ряд Маклорена для функции
Пример 47 Разложить в ряд Маклорена функцию Решение: Аналогично, получим
Применение рядов в приближенных вычислениях
Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения: функций, определенных интегралов. Находятся приближенные решения дифференциальных уравнений.
Пример 48 Вычислить приближенно Решение: Используем ряд Маклорена для функции
подставим
или
получили знакочередующийся ряд, из теоремы Лейбница следует, что погрешность 
то сумма ряда равна
Пример 49 Вычислить интеграл Решение: Используем ряд Маклорена для функции
подставим
вычислим интеграл
Так как четвёртый член ряда меньше заданной точности
Приложения в экономике
Приложения интегрального исчисления в экономике
Пусть функция y=f(t) описывает изменение производительности некоторого производства с течением времени t. Найдем объем продукции u, произведенной за промежуток времени [0,T]. Отметим, что если производительность не изменяется с течением времени (f(t) – постоянная функция), то объем продукции Построим интегральную сумму. Разобьем отрезок [0,T] на промежутки времени точками:
Тогда Перейдя к пределу при
По определению определенного интеграла
таким образом
Итак, если f(t) – производительность труда в момент t, то
Если в функции Кобба-Дугласа считать, что затраты труда есть линейная зависимость от времени, а затраты капитала неизменны, то она примет вид
Определение начальной суммы по ее конечной величине, полученной через время t при годовом проценте p, называется дисконтированием. Задачи такого рода встречаются при определении экономической эффективности капитальных вложений. Пусть Пусть поступающий ежегодно доход изменяется во времени и описывается функцией f(t) и при удельной норме процента, равной i, процент начисляется непрерывно. Можно показать, что в этом случае дисконтированный доход K за время Т вычисляется по формуле:
Пусть известна функция t=t(x), описывающая изменение затрат времени t на изготовление изделия в зависимости от степени освоения производства, где x – порядковый номер изделия в партии. Тогда среднее время, затраченное на изготовление одного изделия в период освоения от
Что касается функции изменения затрат времени на изготовление изделий t=t(x), то часто она имеет вид
где Пример 50 Найти объём продукции, произведённой за 4 года, если функция Кобба-Дугласа имеет вид Решение:
Используем метод интегрирования по частям. Пусть Следовательно,
Пример 51 Определить дисконтированный доход за три года при процентной ставке 8%, если первоначальные (базовые) капиталовложения составили 10 млн. руб., и намечается ежегодно увеличивать капиталовложения на 1 млн. руб. Решение: Очевидно, что капиталовложения задаются функцией
дисконтированная сумма капиталовложений равна:
Вычислим интеграл по частям
Итак, получили
Пример 52 Найти среднее время, затраченное на освоение одного изделия в период освоения от
полагая в формуле Решение:
2.4.2 Приложения дифференциальных уравнений в экономике.
Рассмотрим некоторые задачи макроэкономической динамики.
моменту времени t. Будем полагать, что вся производимая отраслью продукция реализуется по некоторой фиксированной цене p, т.е. выполнено условие ненасыщаемости рынка. Тогда доход к моменту времени t составит Обозначим через I(t) величину инвестиций, направляемых на расширение производства. В модели естественного роста полагают, что скорость выпуска продукции (акселерация) пропорциональна величине инвестиций, имеет место дифференциальное уравнение
Полагая, что величина инвестиций I(t) составляет фиксированную часть дохода, получим
где коэффициент пропорциональности m (так называемая норма инвестиций) – постоянная величина, 0<m<1. Подставляя последнее выражение для I(t) в дифференциальное уравнение, получим Это дифференциальное уравнение – с разделяющимися переменными. Решим его:
При начальных условиях Замечание. Уравнение
только для достаточно узкого времени интервала. В общем случае кривая спроса, т.е. зависимость цены реализованной продукции от ее объема является убывающей функцией p = p(y). Поэтому модель роста в условиях конкурентного рынка примет вид
оставаясь по-прежнему уравнением с разделяющимися переменными. Так как все сомножители в правой части уравнения положительны, то
Так как эластичностьспроса определяется формулой
Условие Таким образом, если спрос эластичен, т.е.
Пример 53 Найти выражение для объёма реализованной продукции Решение: Используя формулу, отражающую модель роста в условиях конкурентного рынка
получим
Решаем: разделим переменные:
интегрируя, получим:
Учитывая, что Таким образом
Пример 54 Найти функцию дохода Решение: Известно, что функция дохода равна
где А также имеет место дифференциальное уравнение
где
Итак, функция дохода удовлетворяет линейному неоднородному уравнению первого порядка. Будем искать его решение в виде Тогда 1)
Общее решение Используя начальные условия Итак, функция дохода имеет вид
стали пользоваться неоклассическими моделями экономического роста, в частности моделями Солоу, в которых коэффициент капиталовооружённости Основное уравнение модели Солоу есть частное дифференциальное уравнение первого порядка
где q – средняя производительность труда ( или стоимость дохода , произведённого одним работающим n – годовой темп прироста населения ( условно 0<n<0,03) Sy – функция сбережения, Данное уравнение показывает, как должна изменяться во времени капиталовооружённость Именно при условии Эту закономерность легко пояснить на графике.
Если левая часть выражения больше правой Напротив, если На рисунке линия
|
|||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 256. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , которую требуется разложить в степенной ряд, т. е. представить в виде
, которую требуется разложить в степенной ряд, т. е. представить в виде
 ряда. Для этого продифференцируем равенство, получим:
ряда. Для этого продифференцируем равенство, получим:
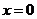 , найдем
, найдем

 в равенства, получим
в равенства, получим


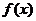 в ряд называется рядом Маклорена, это разложение функции называют разложением по степеням
в ряд называется рядом Маклорена, это разложение функции называют разложением по степеням  .
.

 .
. .
. , поэтому при
, поэтому при  Подставляя эти значения в формулу получим искомое разложение
Подставляя эти значения в формулу получим искомое разложение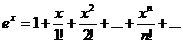
 .
. .
.


 .
.
 , с точностью 0,01.
, с точностью 0,01.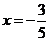 , получим
, получим ,
,
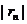 , не превышает первого из отброшенных членов (по абсолютной величине). Так как пятый член ряда меньше заданной точности
, не превышает первого из отброшенных членов (по абсолютной величине). Так как пятый член ряда меньше заданной точности ,
, .
. , с точностью 0,1.
, с точностью 0,1. ,
, , получим
, получим



 , то данный интеграл равен
, то данный интеграл равен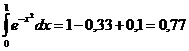
 , произведенной за некоторый промежуток времени
, произведенной за некоторый промежуток времени 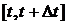 , задается формулой
, задается формулой  .
. . Для величины объема продукции
. Для величины объема продукции  , произведенной за промежуток времени
, произведенной за промежуток времени  , имеем:
, имеем: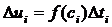 , где
, где 
 .
. .
. , найдем объем произведенной продукции
, найдем объем произведенной продукции .
. ,
, .
. есть объем выпускаемой продукции за промежуток [0,T].
есть объем выпускаемой продукции за промежуток [0,T]. . Тогда объем выпускаемой продукции за T лет составит:
. Тогда объем выпускаемой продукции за T лет составит: (см. Пример 50).
(см. Пример 50). - конечная сумма полученная за t лет, и К – дисконтируемая сумма, которую в финансовом анализе называют также современной суммой. Если проценты простые, то
- конечная сумма полученная за t лет, и К – дисконтируемая сумма, которую в финансовом анализе называют также современной суммой. Если проценты простые, то  - удельная процентная ставка. Тогда
- удельная процентная ставка. Тогда  . В случае сложных процентов
. В случае сложных процентов 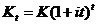 и поэтому
и поэтому  .
.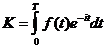 (см. Пример 51).
(см. Пример 51). изделий, вычисляется по теореме о среднем:
изделий, вычисляется по теореме о среднем: .
. ,
, – затраты времени на первое изделие,
– затраты времени на первое изделие,  - показатель производственного процесса. (см. Пример 52).
- показатель производственного процесса. (см. Пример 52).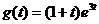 .
.
 ,
,  . Тогда
. Тогда  ,
,  .
.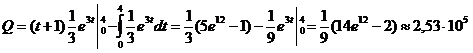 (усл. ед.)
(усл. ед.) . Тогда по формуле:
. Тогда по формуле:
 .
.
 млн. руб. Это означает, что для получения одинаковой наращенной суммы через три года ежегодные капиталовложения от 10 до 13 млн. руб. равносильны одновременным первоначальным вложениям 31 млн. руб. при той же, начисляемой непрерывно, процентной ставке.
млн. руб. Это означает, что для получения одинаковой наращенной суммы через три года ежегодные капиталовложения от 10 до 13 млн. руб. равносильны одновременным первоначальным вложениям 31 млн. руб. при той же, начисляемой непрерывно, процентной ставке. до
до  изделий, используя формулу
изделий, используя формулу ,
, , где
, где  – затраты времени на первое изделие,
– затраты времени на первое изделие,  – показатель производственного процесса,
– показатель производственного процесса,  (мин.),
(мин.),  .
. (мин.).
(мин.). .
.
 ,
, , обозначим k=
, обозначим k=  mp, тогда
mp, тогда  .
.




 решение можно записать в виде
решение можно записать в виде  .
. описывает также рост народонаселения, динамику роста цен при постоянной инфляции, процесс радиоактивного распада и др.
описывает также рост народонаселения, динамику роста цен при постоянной инфляции, процесс радиоактивного распада и др.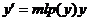
 , и это уравнение описывает возрастающую функцию y(t). При исследовании функции y(t) на выпуклость естественно используется понятие эластичности функции. Дифференцируя уравнение
, и это уравнение описывает возрастающую функцию y(t). При исследовании функции y(t) на выпуклость естественно используется понятие эластичности функции. Дифференцируя уравнение 
 , получим
, получим
 равносильно равенству
равносильно равенству 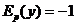 .
. или
или  , то
, то  и функция выпукла вниз; в случае если спрос эластичен, то функция выпукла вверх.
и функция выпукла вниз; в случае если спрос эластичен, то функция выпукла вверх. , если известно, что кривая спроса
, если известно, что кривая спроса  задаётся уравнением
задаётся уравнением  , норма акселерации
, норма акселерации  , норма инвестиций
, норма инвестиций  ,
,  .
.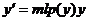 ,
,





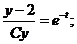

 .
. .
. .
. , если известно, что величина потребления задаётся функцией
, если известно, что величина потребления задаётся функцией  , коэффициент капиталоёмкости прироста дохода
, коэффициент капиталоёмкости прироста дохода  ,
,  .
. ,
, – сумма инвестиций,
– сумма инвестиций,  – величина потребления.
– величина потребления. ,
, , или
, или 
 .
. , подставим в уравнение
, подставим в уравнение 
 2)
2) 





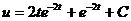
 или
или 
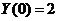 , найдём
, найдём  :
:  или
или  .
. .
. (стоимость основного капитала, приходящаяся на одного занятого в производстве) есть ведичина переменная, меняется в зависимости от состояния экономической коньюнктуры.
(стоимость основного капитала, приходящаяся на одного занятого в производстве) есть ведичина переменная, меняется в зависимости от состояния экономической коньюнктуры. ,
, )
) – инвестиции.
– инвестиции. труда , чтобы существующий равновесный рост обеспечивал полное использование производственных мощностей, и в том числе – полную занятость.
труда , чтобы существующий равновесный рост обеспечивал полное использование производственных мощностей, и в том числе – полную занятость.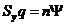 будем иметь место равновесный рост с постоянной капиталовооружённостью и постоянной производительностью труда.
будем иметь место равновесный рост с постоянной капиталовооружённостью и постоянной производительностью труда.
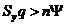 , то сбережения превышают инвестиции, то есть приращение капитала, необходимого для поддержания соответствующего уровня капиталовооружённости
, то сбережения превышают инвестиции, то есть приращение капитала, необходимого для поддержания соответствующего уровня капиталовооружённости  . То есть в этом случае выполняется неравенство
. То есть в этом случае выполняется неравенство  , что требует повышения капиталоёмкости (от
, что требует повышения капиталоёмкости (от  до
до  ).
). , то для достижения равновесия экономики и полной занятости следует понизить капиталовооруженность труда
, то для достижения равновесия экономики и полной занятости следует понизить капиталовооруженность труда  – выпуклая.
– выпуклая.