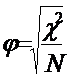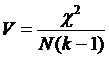При вычислении хи-квадрат для номинальных переменных проверяется нулевая гипотеза о независимости исследуемых переменных, при этом не определяется ни сила, ни направление связи.

⇐ ПредыдущаяСтр 21 из 31Следующая ⇒

Вместе со значением хи-квадрат рассчитывается значение р-уровня значимости.

При р>0,05 cчитается, что различия между наблюдаемыми и ожидаемыми частотами незначительны, нулевая гипотеза о независимости переменных принимается и обосновывается вывод о независимости переменных.

При р<0,05 нулевая гипотеза о независимости переменных отклоняется и обосновывается вывод о зависимости переменных.

Пример:

*Таблица сопряженности Пол сотрудника Категория занятости**
			Категория занятости			Итого
			1 Сотрудник секретариата	2 Сотрудник среднего звена	3 Менеджер	Итого
Пол сотрудника	1 жен	Частота	157	27	74	258
	1 жен	Ожидаемая частота	197,6	14,7	45,7	258,0
	2 муж	Частота	206	0	10	216
	2 муж	Ожидаемая частота	165,4	12,3	38,3	216,0
Итого		Частота	363	27	84	474
Итого		Ожидаемая частота	363,0	27,0	84,0	474,0

Наблюдаемые частоты отличны от ожидаемых, поэтому предполагаем зависимость между переменными.

Критерии хи-квадрат
				Знч. Монте-Карло (2-стор.)			Знч. Монте-Карло (1-стор.)
					99% доверительный интервал			99% доверительный интервал
	Значение	ст.св.	Асимпт. значимость (2-стор.)	Знч.	Нижняя граница	Верхняя граница	Знч.	Нижняя граница	Верхняя граница
Хи-квадрат Пирсона	79,277^a	2	,000	,000^b	,000	,000
Отношение правдоподобия	95,463	2	,000	,000^b	,000	,000
Точный критерий Фишера	90,869			,000^b	,000	,000
Линейно-линейная связь	67,463^c	1	,000	,000^b	,000	,000	,000^b	,000	,000
Кол-во валидных наблюдений	474
a. В 0 (,0%) ячейках ожидаемая частота меньше 5. Минимальная ожидаемая частота равна 12,30.
b. На основании 10000 случайных таблиц с начальным значением 2000000 датчика случайных чисел.
c. Стандартизованная статистика равна -8,214.

Действительно, р=0,000 – наличие связи.

Так как значение хи-квадрат определяется объемом выборки, сравнение двух значений хи-квадрат, полученных при разных условиях, становится бессмысленным.

К. Пирсон предложил рассечет коэффициента фи с целью более наглядной интерпретации связи

Коэффициент j как изменяется от 0 (независимые переменные) до 1. Однако, если одна из переменных имеет более двух градаций, значение фи может превышать значение в единицу. В этом случае может быть использован к. Крамера, который может принимать значения от единицы (строго связанные переменные) до нуля (для независимых переменных).

k – наименьшее из чисел градаций двух переменных,

N – размер выборки

В примере значение этих коэффициентов также свидетельствует о наличии связи.

Симметричные меры
				Знч. Монте-Карло
					99% доверительный интервал
		Значение	Прибл. значимость	Знч.	Нижняя граница	Верхняя граница
Номинальная по номинальной	Фи	,409	,000	,000^a	,000	,000
Номинальная по номинальной	V Крамера	,409	,000	,000^a	,000	,000
Кол-во валидных наблюдений		474
a. На основании 10000 случайных таблиц с начальным значением 2000000 датчика случайных чисел.

Ошибка первого рода – когда нулевая гипотеза отвергается, хотя она верна.

Вероятность допустить ошибку первого рода равна вероятности ошибки р.

Уровень статистической значимости

Вероятность допустить ошибку первого рода	Значение р	интерпретация
5%	р<0,05	низший уровень статистической значимости
1%	p<0,01	достаточный уровень статистической значимости
0,1%	p<0,001	высокий уровень статистической значимости

⇐ Предыдущая 16 17 18 19 202122 23 24 25 Следующая ⇒

Последнее изменение этой страницы: 2018-04-12; просмотров: 390.

stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда...