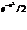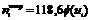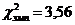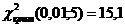Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Алгоритм применения критерия хи-квадрат Пирсона для сопоставления эмпирического и теоретического (другого эмпирического) распределений одного признака1. Рассчитать эмпирическое значение хи-критерия и сравнить его значение с критическим значением для соответствующего уровня значимости α и данного числа степеней свободы r=m-1 ( m - количество строк в таблице). 2. Если эмпирическое значение хи-критерия превышает критическое значение, то расхождения между распределениями существенны на данном уровне значимости. Пример: при изучении творческой активности студентов были получены результаты для экспериментальных и контрольных групп. Определите, являются ли значимыми результаты предложенного подхода.
c2эмп=25,32 c2кр=9,21 для α=0,01 и r=2 Нулевая гипотеза опровергается на высоком уровне значимости, что позволяет признать, что разница частот контрольного и экспериментального ряда является статистически достоверной. Пример: в банке в течение двух дней проводилось исследование времени обслуживания клиентов, результаты приведены ниже. Можно ли считать одинаковыми среднее время обслуживания клиентов банка в первый и второй дни при уровне значимости в 0,05?
По таблице критических точек распределения хи-квадрат для α=0,05 и числу степеней свободы k=n-1=6 находим критическую точку  Нет оснований отвергать нулевую гипотезу об одинаковом времени обслуживания клиентов банка в разные дни. Проверка гипотезы о нормальном распределении генеральной совокупности. Пример: в результате выборочного обследования стажа работы профессорско-преподавательского состава получены данные, представленные в таблице. Известно значение выборочной дисперсии Ϭ=5,43 и n=161 – объем выборки. Выяснить, является ли распределение стажа работы нормальным при уровне значимости α=0,01 .
Перейдем от заданного интервального распределения к распределению равноотстоящих вариант и вычислим выборочное среднее и выборочное среднее квадратическое отклонение.
Составим расчетную таблицу
при уровне значимости α=0,01 и числу степеней свободы k=s-3=8-3=5 Гипотезу о нормальном распределении генеральной совокупности принимаем. Распределение Стьюдента (t-pаспределение) c k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента приближается к нормальному. Алгоритм применения t-критерия Стьюдента для сравнения оценки средних величин двух выборок 1. Записать вариационный ряд результатов x экспериментальной группы и y контрольной группы. 2. Найти выборочные средние и выборочные дисперсии 3. Вычислить эмпирическое значение критической статистики и сравнить его с критическим значением tкрит
n и m – число ячеек для переменных x и y соответственно Критическое значение tкрит определяется по таблице для уровня значимости α и степеней свободы r=n+m-2 . Если tэьпир>tкрит, то различия между средними значениями экспериментальной и контрольной групп существенны на данном уровне значимости. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 596. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
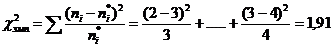
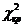 =14,1.
=14,1.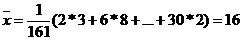
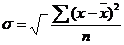 =5,43,
=5,43, 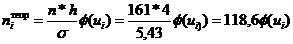 –теоретические частоты, n=161 – объем выборки
–теоретические частоты, n=161 – объем выборки 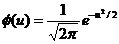 ui=( xi-
ui=( xi- 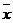 )/Ϭ
)/Ϭ