
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сравнение двух средних нормальных генеральных совокупностей.Пример: для представленных данных, используя t-критерий Стьюдента на 1%-м уровне значимости, докажите достоверность различия между средними величинами опыта и контроля.
Проверка гипотезы о значимости выборочного коэффициента корреляции (нулевая гипотеза - равенство нулю коэффициента корреляции) Пример: определите, существует ли корреляционная связь между рождаемостью и смертностью для городов Ярославской области.
Вычислим выборочную ковариацию k(x,y)=1/6[(104,9-11,6)*(103,4-104,7) + (119,3-11,6)*(105,9-104,7)]= -0,7
Вычислим наблюдаемое значение критерия
Для уровня значимости в 0,1 и степеней свободы r=n-2=4
Вопросы для самоконтроля 1. Назовите основные типы статистических критериев проверки гипотезы. 2. В каких случаях применяются критерии Стьюдента и Пирсона? 3. Как определяются степени свободы? 4. Какие выборки следует считать однородными? 5. Какие критерии однородности вы знаете? Каковы условия применимости этих критериев? 6. Почему в критерии хи- Пирсона не может быть недопустимо малых значений критической статистики? 7. Коэффициенты ранговой корреляции Спирмена, Кендалла и критические точки распределения Стьюдента.  8. Приведите примеры практических задач, когда необходима проверка гипотез о равенстве математических ожиданий, дисперсий. |
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 712. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

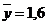
 7
7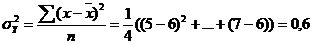
 =
= 


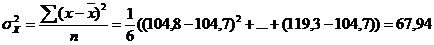 ,
, 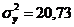


 – нет оснований отвергать нулевую гипотезу (r =0).
– нет оснований отвергать нулевую гипотезу (r =0).