Студопедия

КАТЕГОРИИ:

АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Ошибка второго рода – когда нулевая гипотеза принимается, хотя она ложна.

⇐ ПредыдущаяСтр 22 из 31Следующая ⇒

Вероятность ошибки второго рода тем меньше, чем больше вероятность ошибки р. Вероятности ошибки, при которой допустимо отвергнуть нулевую гипотезу и принять альтернативную гипотезу, зависит от каждого конкретного случая. В значительной степени эта вероятность определяется характером исследуемой ситуации.

Чем больше требуемая вероятность, с которой надо избежать ошибочного решения, тем более узкими выбираются границы вероятности ошибки, при которой отвергается нулевая гипотеза, так называемый доверительный интервал вероятности.

Значение критерия хи-квадрат в значительной степени определяется количеством ячеек таблицы сопряженности и объемом выборки, поэтому сопоставление двух значений хи-квадрат, полученных при разных условиях, становится бессмысленным.

Таблицы сопряженностистроятся через меню Описательные статистики / Таблицы сопряженности.

Диалоговое окно Таблицы сопряженности позволяет определить одну или несколько переменных в состав таблицы, а также осуществить вывод столбиковой диаграммы. Обычно в строки помещают независимую переменную, а в столбцы – зависимую.

Область Слой позволяет вложить одну переменную в состав другой, таким образом, построить таблицу для трех и более переменных.  

Например: ф . Служащие.

Определим переменную «пол»– в строки, переменную «зрение» – в столбцы, а переменную «категория занятости»  – в слои, а то для каждой категории занятости будут созданы вложенные слои для мужчин и женщин отдельно.

 

Таблица сопряженности Пол сотрудника * заболевание * Категория занятости

Категория занятости

заболевание

Итого
1,00 в норме 2,00 нарушение зрения

1 Сотрудник секретариата

Пол сотрудника

1 жен

 Частота 45 111 156
Ожидаемая частота 57,3 98,7 156,0
% в заболевание 33,8% 48,5% 43,1%

2 муж

 Частота 88 118 206
Ожидаемая частота 75,7 130,3 206,0
% в заболевание 66,2% 51,5% 56,9%

Итого

 Частота 133 229 362
Ожидаемая частота 133,0 229,0 362,0
% в заболевание 100,0% 100,0% 100,0%

2 Сотрудник среднего звена

Пол сотрудника

1 жен

 Частота 1 18 19
Ожидаемая частота ,7 18,3 19,0
% в заболевание 100,0% 69,2% 70,4%

2 муж

 Частота 0 8 8
Ожидаемая частота ,3 7,7 8,0
% в заболевание ,0% 30,8% 29,6%

Итого

 Частота 1 26 27
Ожидаемая частота 1,0 26,0 27,0
% в заболевание 100,0% 100,0% 100,0%

3 Менеджер

Пол сотрудника

1 жен

 Частота 54 20 74
Ожидаемая частота 56,4 17,6 74,0
% в заболевание 84,4% 100,0% 88,1%

2 муж

 Частота 10 0 10
Ожидаемая частота 7,6 2,4 10,0
% в заболевание 15,6% ,0% 11,9%

Итого

 Частота 64 20 84
Ожидаемая частота 64,0 20,0 84,0
% в заболевание 100,0% 100,0% 100,0%

 

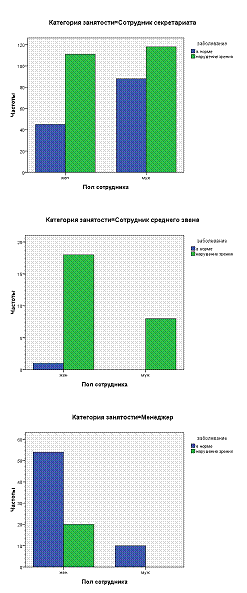
    Значение критерия рассчитывается отдельно для каждого слоя

Критерии хи-квадратh

Категория занятости

 Значение ст.св. Асимпт. значимость (2-стор.) Точная значимость (2-стор.) Точная значимость (1-стор.) Вероятность в точке

1 Сотрудник секретариата

 Хи-квадрат Пирсона 7,350a 1 ,007 ,008 ,004  
Поправка на непрерывностьb 6,766 1 ,009      
Отношение правдоподобия 7,441 1 ,006 ,008 ,004  
Точный критерий Фишера       ,008 ,004  
Линейно-линейная связь 7,330c 1 ,007 ,008 ,004 ,002
Кол-во валидных наблюдений 362          

2 Сотрудник среднего звена

 Хи-квадрат Пирсона ,437d 1 ,508 1,000 ,704  
Поправка на непрерывностьb ,000 1 1,000      
Отношение правдоподобия ,719 1 ,397 1,000 ,704  
Точный критерий Фишера       1,000 ,704  
Линейно-линейная связь ,421e 1 ,516 1,000 ,704 ,704
Кол-во валидных наблюдений 27          

3 Менеджер

 Хи-квадрат Пирсона 3,547f 1 ,060 ,108 ,055  
Поправка на непрерывностьb 2,214 1 ,137      
Отношение правдоподобия 5,849 1 ,016 ,065 ,055  
Точный критерий Фишера       ,108 ,055  
Линейно-линейная связь 3,505g 1 ,061 ,108 ,055 ,055
Кол-во валидных наблюдений 84          

a. В 0 (,0%) ячейках ожидаемая частота меньше 5. Минимальная ожидаемая частота равна 57,31.

b. Вычисляется только для таблицы 2x2.

c. Стандартизованная статистика равна -2,707.

d. В 2 (50,0%) ячейках ожидаемая частота меньше 5. Минимальная ожидаемая частота равна ,30.

e. Стандартизованная статистика равна ,649.

f. В 1 (25,0%) ячейках ожидаемая частота меньше 5. Минимальная ожидаемая частота равна 2,38.

g. Стандартизованная статистика равна -1,872.

h. Для таблицы сопряженности 2x2 вместо результатов Монте-Карло даются точные результаты.

 

 

       В этом случае столбиковые диаграммы выводятся отдельно для каждого слоя.

 

    Назначение кнопок диалогового окна.

    1. кн. Ячейки определяет по умолчанию наблюдаемые частоты, могут быть восстановлены значения ожидаемых частот (в количественном или процентном соотношении. В случае, если данные представлены в процентах, возможен выбор способа подсчета.

Проценты по столбцам будут подсчитываться частота ячейки в процентах от суммарной частоты столбца.

Проценты по строкам – частота ячейки в процентах от суммарной частоты столбца.

Проценты по таблице – частота ячейки в процентах от суммарной частоты всей таблицы (от общего числа респондентов).

При помощикн. Ячейки могут быть выставлены Нестандартизированные остатки как разность наблюдаемых и ожидаемых частот. Стандартизированные остатки – разность наблюдаемых и ожидаемых частот, деленная на корень из ожидаемых частот.

Таблица сопряженности материальное положение * Размер взятки
     

Размер взятки

Итого
      1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

материальное положение

1 Недоволен материальным положением

 Частота 3 3 3 3 3 3 3 3 3 3 30
Ожидаемая частота 3,0 3,0 3,0 3,0 3,0 3,0 3,0 3,0 3,0 3,0 30,0
Остаток ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0  

2 Доволен материальным положением

 Частота 3 3 3 3 3 3 3 3 3 3 30
Ожидаемая частота 3,0 3,0 3,0 3,0 3,0 3,0 3,0 3,0 3,0 3,0 30,0
Остаток ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0  

Итого

 Частота 6 6 6 6 6 6 6 6 6 6 60
Ожидаемая частота 6,0 6,0 6,0 6,0 6,0 6,0 6,0 6,0 6,0 6,0 60,0

 

Остатки наглядно свидетельствуют об отсутствии связи.

3. кн. Статистики – вычисляются статистические критерии для переменных, относящихся к номинальной, порядковой и к интервальной шкале (хи-квадрат, коэффициенты фи и Крамера).




⇐ Предыдущая17181920212223242526Следующая ⇒






Последнее изменение этой страницы: 2018-04-12; просмотров: 408.

stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда...