Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ГЛАВА 3. ДИСКРЕТНЫЕ СТРУКТУРЫ: КОНЕЧНЫЕ АВТОМАТЫ, КОДЫМашина Тьюринга Машина Тьюринга – это абстрактная структура, пример алгоритма. Машина Тьюринга (МТ) состоит из: · управляющего устройства, которое может находиться в одном из состояний, образующих конечное множество · ленты, разбитой на ячейки, в каждой из которых может быть записан один из символов конечного алфавита · устройства обращения к ленте, т. е. считывающей и пишущей головки, которая в каждый момент времени обозревает ячейку ленты, в зависимости от символа в этой ячейке и состояния управляющего устройства записывает в ячейку символ (может быть, совпадающий с прежним или пустой, т.е. стирает символ), сдвигается на ячейку влево, или вправо, или остается на месте; при этом управляющее устройство переходит в новое состояние или остается в прежнем состоянии. Лента бесконечна в обе стороны, однако, в начальный момент времени только конечное число ячеек ленты заполнены. Поэтому важна не фактическая бесконечность ленты, а ее неограниченность, т. е. возможность писать на ней сколь угодно длинные конечные слова. Среди состояний управляющего устройства выделены начальное состояние Для любого состояния · следующее состояние · символ · направление сдвига головки Это задание может записываться либо системой команд, имеющих вид 
либо таблицей, строкам которой соответствуют состояния, столбцам – входные символы, а на пересечении строки Полное состояние МТ, по которому однозначно можно определить ее дальнейшее поведение определяется состоянием управляющего устройства, словом, записанным на ленте, положением считывающей и пишущей головки. Полное состояние называется конфигурацией. Конфигурация обозначается тройкой Ко всякой незаключительной конфигурации Для вычисления функций типа Правильная запись данных на ленте предполагает, что каждое слово, представленное в унарном коде будет записано последовательностью единиц, заполняющих подряд идущие ячейки, между словами ставится разделитель ( символ, отличный от 1), не являющийся пустым символом, левее первого пустого и правее последнего пустого символа на ленте нет непустых ячеек. Таким образом, в начальном состоянии МТ обозревает первую непустую ячейку на ленте. Аналогично, для заключительного состояния. Пустой символ может встречаться внутри слова в процессе работы МТ, выполняя вспомогательную функцию, но не в исходных данных и не в конечном результате. Пример. Записать систему команд, реализующих функцию Слагаемые х и у являются натуральными числами и представлены на ленте в унарном коде. Между последовательностями х единиц и у единиц стоит разделитель: Данная последовательность действий описывается следующей системой команд:
Если МТ видит в первой ячейке разделитель, значит Заметим, что данная система команд могла бы быть короче, если бы мы не задались целью, закончить работу МТ в той же ячейке ленты, в которой начали. Это бывает необходимо, если МТ работает не с целой лентой, а лишь с полулентой (лентой, бесконечной лишь в одну сторону). Такое встречается, если при построении композиции МТ, необходимо сохранить результат, полученный при работе предыдущей МТ. Применим данную систему команд к стандартной начальной конфигурации
УПРАЖНЕНИЯ 1. Осуществить сдвиг данной последовательности единиц на одну ячейку вправо; на две ячейки влево. 2. Построить машину Тьюринга для функции типа 1) 3) 3. Построить машину Тьюринга для функции типа 1) 3) 4. Построить машину Тьюринга для функции 5. Найти целую часть числа х, где 6. Построить машину Тьюринга для функции-разветвления типа 1) 3) 5)
Основы теории кодирования Кодомназывается система условных знаков (символов), для передачи, обработки и хранения информации. Пусть А – произвольный алфавит. Элементы алфавита А называются буквами, а конечные вектора, составленные из букв – словами. Длина слова – число букв в слове Соединение слов Рассмотрим алфавит Произвольное отображение произвольного множества М в множество слов в алфавите При k = 2, Пример 1. Кодирование (отображение) Е – двоичная запись натуральных чисел с помощью минимального количества букв. Числу
наименьшей длины, удовлетворяющее условию:
При этом
Пусть n = 12.
Аналогично
Таким образом, двоичный код числа 12 имеет вид:
Пример 2. Кодирование Числу
ставится в соответствие слово
Пусть n = 12, m = 3. Так как неверно то, что Пусть n = 12, m = 6. Так как верно то, что
Побуквенное кодирование – это кодирование слов в алфавите А таким образом, что сначала кодируются буквы алфавита Код называется разделимым, если разным словам в алфавите А всегда соответствуют разные слова в алфавите V. Утверждение 1. Побуквенное кодирование является взаимно однозначным тогда и только тогда, когда оно задается с помощью разделимого кода. Равномерный код – это код, в котором все кодовые слова имеют одинаковую длину. Утверждение 2. Равномерный код всегда разделим. Код называется префиксным, если никакое кодовое слово из V не является началом другого кодового слова. Утверждение 3. Префиксный код всегда является разделимым, но разделимый код не обязательно является префиксным. Т. е. префиксность является достаточным условием разделимости, но не является необходимым условием. Пусть источник случайным образом генерирует буквы алфавита
Так как алфавит фиксирован, то это распределение можно записать в виде: Стоимостью кода V при распределении P назовем число
Оно характеризует среднее количество букв кодирующих слов, приходящихся на одну букву алфавита А при кодировании V. Очевидно, что при различных кодированиях одного и того же алфавита, стоимость кодов будет различной. Префиксный код Пример 3. Код Р. Фано, близкий к оптимальному, заключается в следующем. Упорядоченный (в порядке не возрастания вероятностей) список букв алфавита делится на две последовательные части так, чтобы суммы вероятностей входящих в них букв отличались как можно меньше. Буквам из 1-ой части присваивается символ 0, из 2-ой – 1. С каждой частью поступают аналогично. Так делается пока, в каждой из частей не окажется по одной букве. Полученные последовательности нулей и единиц является кодом Фано данного алфавита.
В таблице приведен пример построения кода Фано для распределения Р = {0.30, 0.18, 0.14, 0.14, 0.11, 0.06, 0.05, 0.02}.
Найдем стоимость полученного кода.
Теорема Хаффмена Если
то код
Код Пример 4. Построение оптимального кода Хаффмена заключаются в следующем. Пусть в упорядоченном по невозрастанию вероятностей списке две последние вероятности Ниже приведен пример построения кода Хаффмена для распределения Р = {0.5, 0.2, 0.2, 0.1}.
Найдем стоимость полученного кода.
Рассмотрим равномерный код с обнаружением и исправлением ошибок. Однозначной ошибкойтипазамещения называют результат замены одного из символов 0 на 1 или 1 на 0. Кратностью ошибки s называется число ошибок одного типа. Например, если передаваемое слово Функция Хемминга Здесь l – та длина двоичного кода, которой достаточно, чтобы закодировать номера всех координат слова х.
Таким образом,
Пример 5. Найти функцию Хемминга для двоичного слова
Тогда = Кодом Хемминга называется подмножество двоичных слов Утверждение. Количество двоичных слов Теорема Хемминга Код Хемминга является кодом с исправлением одного замещения. Пример 6. Пусть при передаче по каналу связи в двоичном слове
Полученный результат является двоичным кодом номера того места, на котором произошло замещение. УПРАЖНЕНИЯ 1. Записать коды Е для следующих чисел: 29, 43, 85, 120, 167.
2. Выяснить, возможно ли построение кодов Е4, Е5, Е6 для чисел 11, 33, 92, 111. Построить существующие коды.
3. Найти коды Е4 для чисел 9, 10, 13, 15 используя лексикографический порядок.
4. Найти код Е для чисел 17, 35, 62, 126, 259 используя лексикографический порядок.
5. Построить для следующего распределения вероятностей код Фано. Найти стоимость кода.
6. Построить для следующего распределения вероятностей код Хаффмена. Найти стоимость кода.
7. Построить для данного распределения частот коды Фано и Хаффмена. Сравнить стоимости кодов.
8. Являются ли элементами множества кодовых слов Хемминга (элементами кода Хемминга) Нn следующие слова: 1) n=4, 101; 2) n=5, 01010; 3) n=8, 11010110; 4) n=11, 00110100110.
9. Найти множество всех кодовых слов Нn для n = 3, 4, 5.
10. Закодировать по Хеммингу слова: 1) 1011; 2) 1110; 3) 100100; 4) 101101100; 5) 0001110110. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 359. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ;
; ;
; и заключительное состояние
и заключительное состояние  . В начальном состоянии МТ находится перед началом работы, попав заключительное состояние МТ останавливается.
. В начальном состоянии МТ находится перед началом работы, попав заключительное состояние МТ останавливается. и символа
и символа  однозначно заданы:
однозначно заданы: ;
; , который нужно записать вместо
, который нужно записать вместо  );
);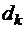 ,обозначаемое одним из трех символов: L – влево, R – вправо, E – на месте.
,обозначаемое одним из трех символов: L – влево, R – вправо, E – на месте.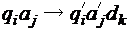 ,
, . Еще возможен графический способ задания.
. Еще возможен графический способ задания. , где
, где 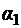 – слово, слева от головки,
– слово, слева от головки,  – слово, образованное символом, обозреваемым головкой и символами справа от него. Стандартная начальная конфигурация имеет вид
– слово, образованное символом, обозреваемым головкой и символами справа от него. Стандартная начальная конфигурация имеет вид  , т.е. головка обозревает крайний левый символ, записанный на ленте. Стандартная заключительная конфигурация имеет вид
, т.е. головка обозревает крайний левый символ, записанный на ленте. Стандартная заключительная конфигурация имеет вид 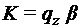 , т. е. головка обозревает крайний левый символ результирующего слова. Это делается для того, чтобы вслед за этой МТ могла работать другая МТ, для которой данная заключительная конфигурация будет начальной. Таким образом строится композиция МТ.
, т. е. головка обозревает крайний левый символ результирующего слова. Это делается для того, чтобы вслед за этой МТ могла работать другая МТ, для которой данная заключительная конфигурация будет начальной. Таким образом строится композиция МТ. применима ровно одна команда вида
применима ровно одна команда вида  . Это обозначается
. Это обозначается 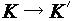 . Если существует последовательность конфигураций
. Если существует последовательность конфигураций 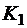 ,
, 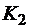 , ... , переводящих
, ... , переводящих  , так что
, так что  , то это обозначается
, то это обозначается  . Так если
. Так если  – стандартная начальная конфигурация, а
– стандартная начальная конфигурация, а 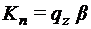 – стандартная заключительная конфигурация, то правильно построенная МТ должна
– стандартная заключительная конфигурация, то правильно построенная МТ должна  .
. используется запись на ленте в унарном коде, т. е. натуральное число представляется последовательностью единиц, записанных подряд. Например, число хпредставлено в виде слова 11...1=
используется запись на ленте в унарном коде, т. е. натуральное число представляется последовательностью единиц, записанных подряд. Например, число хпредставлено в виде слова 11...1=  , состоящего из х единиц.
, состоящего из х единиц.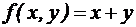 .
. . Это машинное слово (последовательность символов) надо переработать в слово
. Это машинное слово (последовательность символов) надо переработать в слово 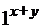 , состоящее из
, состоящее из  единиц, идущих подряд. Очевидно, что для этого необходимо заменить разделитель единицей, стереть (заменить пустым символом) последнюю единицу справа, вернуться на первую слева непустую ячейку.
единиц, идущих подряд. Очевидно, что для этого необходимо заменить разделитель единицей, стереть (заменить пустым символом) последнюю единицу справа, вернуться на первую слева непустую ячейку. ;
;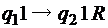 ;
; ;
; ;
; ;
;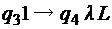
 ;
;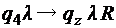 .
. . МТ заменяет разделитель на 1, тем самым единиц становится на одну больше, чем надо, ведь результат равен у. Тогда МТ доходит в состоянии
. МТ заменяет разделитель на 1, тем самым единиц становится на одну больше, чем надо, ведь результат равен у. Тогда МТ доходит в состоянии  до конца слова и стирает в состоянии
до конца слова и стирает в состоянии  последнюю единицу. В состоянии
последнюю единицу. В состоянии 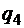 осуществляется обратный проход до первой пустой слева ячейки. Если же в первой ячейке МТ видит 1, то сначала в состоянии
осуществляется обратный проход до первой пустой слева ячейки. Если же в первой ячейке МТ видит 1, то сначала в состоянии 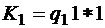 . МТ должна преобразовать сумму двух единиц в два.
. МТ должна преобразовать сумму двух единиц в два.

 ; 2)
; 2) 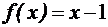 ;
; ; 4)
; 4)  .
.
 ;
; ; 4)
; 4)  .
. , где
, где 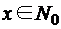 .
.
 ; 2)
; 2) 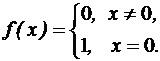 ;
; ; 4)
; 4)  ;
; ; 6)
; 6) 
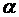 , обозначается
, обозначается 
 и
и  обозначим через
обозначим через 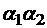 , а соединение n одинаковых слов
, а соединение n одинаковых слов  . Слово
. Слово  .
.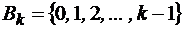 .
.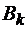 называется k-ичным кодированием множества М.
называется k-ичным кодированием множества М. – двоичное множество.
– двоичное множество.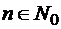 ставится в соответствие слово
ставится в соответствие слово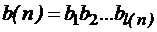 ,
, .
. , а длина слова
, а длина слова  . Последнее условие означает, что n удовлетворяет неравенству
. Последнее условие означает, что n удовлетворяет неравенству .
.
 , т. е. это дробное число между 3 и 4. Инкремент этого логарифма равен
, т. е. это дробное число между 3 и 4. Инкремент этого логарифма равен  , так как это следующее целое, идущее за ним.
, так как это следующее целое, идущее за ним.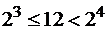 . Значит,
. Значит, 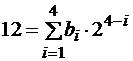 .
.
 .
.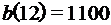 .
. – двоичная запись натуральных чисел с помощью m букв.
– двоичная запись натуральных чисел с помощью m букв.
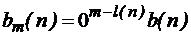 .
. , то это означает, что код
, то это означает, что код  построить невозможно.
построить невозможно.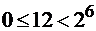 , то это означает, что код
, то это означает, что код  .
.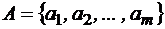 двоичными словами из множества кодовых слов
двоичными словами из множества кодовых слов  , а затем уже слово, составленное в алфавите А заменяется последовательностью кодовых слов, соответствующих его буквам. Пример побуквенного кодирования слов – азбука Морзе.
, а затем уже слово, составленное в алфавите А заменяется последовательностью кодовых слов, соответствующих его буквам. Пример побуквенного кодирования слов – азбука Морзе.

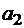
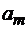


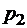
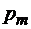
 .
.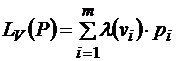 .
. , если его стоимость минимальна по сравнению с другими кодами алфавита А при распределении Р.
, если его стоимость минимальна по сравнению с другими кодами алфавита А при распределении Р.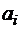




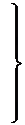


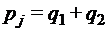 , причем
, причем ,
, так же является оптимальным при распределении
так же является оптимальным при распределении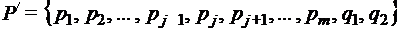 .
. является расширением кода
является расширением кода  .
.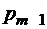 и
и  . Эти вероятности из списка исключаются, а их сумма вставляется в список таким образом, чтобы вероятности по-прежнему не убывали. Делаем так, пока в списке не останется две вероятности. Первой из них присваивается символ 0, второй – символ 1. Получаем оптимальный код, состоящий из 2 кодовых слов. Далее, используя теорему расширяем его до кода из 3 слов, и т. д. Пока не получим список исходных вероятностей.
. Эти вероятности из списка исключаются, а их сумма вставляется в список таким образом, чтобы вероятности по-прежнему не убывали. Делаем так, пока в списке не останется две вероятности. Первой из них присваивается символ 0, второй – символ 1. Получаем оптимальный код, состоящий из 2 кодовых слов. Далее, используя теорему расширяем его до кода из 3 слов, и т. д. Пока не получим список исходных вероятностей.











 .
. , а на приемной станции получено
, а на приемной станции получено 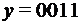 , то в слове произошла ошибка типа замещения.
, то в слове произошла ошибка типа замещения.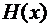 , задается на двоичных векторах
, задается на двоичных векторах 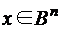 . Это вектор минимальной длины l, полученный в результате покоординатного сложения по модулю 2 двоичных кодов номеров тех координат вектора х, которые равны 1.
. Это вектор минимальной длины l, полученный в результате покоординатного сложения по модулю 2 двоичных кодов номеров тех координат вектора х, которые равны 1. .
.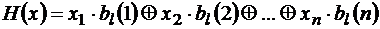 .
.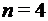 , то
, то  . Найдем двоичные коды длины 3 для всех номеров координат слова х .
. Найдем двоичные коды длины 3 для всех номеров координат слова х .
 =
=  =
=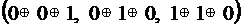 =
=  .
. , для каждого из которых функция Хемминга равна нулевому вектору. Таким образом
, для каждого из которых функция Хемминга равна нулевому вектору. Таким образом 
 .
.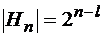 .
. произошло замещение 5-ого символа, в результате чего получилось слово
произошло замещение 5-ого символа, в результате чего получилось слово  . Найдем функцию Хемминга
. Найдем функцию Хемминга  .
. 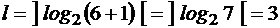 . Сложим по модулю 2 двоичные коды номеров только тех координат вектора у, которые равны 1.
. Сложим по модулю 2 двоичные коды номеров только тех координат вектора у, которые равны 1. .
.