
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Минимизация ДНФ. Тупикова ДНФДаже если ДНФ сокращенная, ее можно минимизировать, то есть уменьшить количество входящих в нее элементарных конъюнкций. Пример. Пусть сокращенная ДНФ функции имеет вид:
Тогда ее единичное множество может быть представлено в виде:
Заметим, что наборы, входящие в последнее подмножество, находятся так же в первом и во втором. Так Сокращенная ДНФ, из которой удалены все лишние импликанты, называется тупиковой.
Отношение покрытия между единичными наборами и импликантами ДНФ наглядно задается таблицей покрытия. Строки таблицы соответствуют конъюнкциям ДНФ, столбцы – элементам единичного множества. На пересечении строки и столбца ставится пометка, если данная конъюнкция обращается в единицу данным набором значений аргументов (иначе говоря, данный набор покрывается единичным множеством конъюнкции). Пример. Пусть ДНФ функции имеет вид:
Тогда ее единичное множество может быть представлено в виде:
Построим таблицу покрытия.
Из таблицы видно, что вторая строчка – лишняя, то есть если ее убрать, все элементы единичного множества останутся покрыты. Значит, импликант Так бывает не всегда.  Замечание.1 Чтобы с помощью таблицы покрытия получить тупиковую ДНФ, необходимо сначала получить сокращенную ДНФ и именно ее простые импликанты помещать в таблицу покрытия. Замечание.2 У функции может быть несколько тупиковых ДНФ. Чтобы найти их необходимо построить сокращенную ДНФ, содержащую все простые импликанты данной функции. Метод Блейка-Порецкого – метод получения сокращенной ДНФ, содержащей все простые импликанты. Пусть дана СДНФ функции. 1. Перенумеруем элементарные конъюнкции. 2. Осуществим попарно склеивание каждой конъюнкции с каждой, если это возможно. Под полученными конъюнкциями будем фиксировать номера. 3. Допишем к списку полученных конъюнкций те, которые не участвовали в склеивании (их номера не фиксировались). 4. Вернемся к п.1. В результате получим сокращенную ДНФ, содержащую все простые импликанты. Пример. Дана СДНФ вида:
Получить с помощью метода Блейка-Порецкого сокращенную ДНФ, содержащую все простые импликанты.
П. 1. П. 2, 3. П.4. Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: Построим таблицу покрытия:
Из таблицы видно, что первую строку удалять нельзя, так как при этом останется не покрыт набор 001. Вторую строку можно удалить, так как наборы, составляющие единичное множество конъюнкции Таким образом, дана функция имеет 2 тупиковые ДНФ:
Пример 2.
П. 1. П. 2, 3. П.4. Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: Построим таблицу покрытия:
Из таблицы видно, что при удалении любой ее строки появятся единичные наборы, не покрытые никаким единичным множеством. Следовательно, полученная сокращенная ДНФ является тупиковой.
УПРАЖНЕНИЯ 1. Проверить с помощью таблицы покрытия, нет ли лишних импликантов среди конъюнкций следующей ДНФ: 1) 2) 3) 4)
2. Получить сокращенную ДНФ функции методом Блейка-Порецкого. Из сокращенной ДНФ получить тупиковую ДНФ с помощью таблицы покрытия. 1) 2) 3) 4) 5) 6) 7)
3. Упростить ДНФ с помощью эквивалентных преобразований. Получить из нее сокращенную ДНФ заменой импликантов на простые. Получить тупиковую ДНФ с помощь. Таблицы покрытия. 1) 2) 3) 4) 5) 6)
4. Функция f(x, y, z) задана таблицей. Записать ее тупиковую ДНФ, используя соответствие между конъюнкциями ДНФ и их интервалами.
5. Не полностью определенная функция f(x, y, z) задана таблицей. Доопределить ее так, чтобы ДНФ имела как можно более простой вид.
Алгебра Жегалкина Алгеброй Жегалкина называется алгебра вида 1) коммутативность сложения по модулю 2
2) ассоциативность сложения по модулю 2
3) дистрибутивность конъюнкции по отношению к сложению по модулю 2
4) а также все тождества, истинные для конъюнкции. От любой булевой формулы можно перейти к формуле алгебры Жегалкина, используя тождества:
Полином Жегалкина – это формула алгебры Жегалкина, имеющая вид суммы по модулю 2 элементарных конъюнкций различного количества переменных без отрицаний. Линейной функцией называется функция, полином Жегалкина которой имеет вид:
где, УПРАЖНЕНИЯ 1. Привести функцию, заданную булевой формулой, к полиному Жегалкина. Проверить, обладает ли она свойством линейности. 1) 2) 3) 4) 5) 6) 7)
2. Привести функцию к полиному Жегалкина. Проверить, обладает ли она свойством линейности. 1) 2) 3) 4) 5)
3. Получить суперпозицию линейных функций f(x, y, z), g(x, y, z), h(x, y, z). Убедится в том, что полученная суперпозиция будет линейной функцией, где 1) 3)
Двойственность Функция Чтобы получить двойственную функцию из исходной, надо каждой переменной придать отрицание на самом нижнем уровне формулы, затем общее отрицание всей формуле (на самом верхнем уровне) и привести к ДНФ (упростить). У двойственной функции на противоположных наборах принимаются противоположные значения: если Функция Самодвойственными являются функции Вектор-столбец самодвойственной функции антисимметричен относительно своей середины (при лексикографическом порядке аргументов). Принцип двойственности Если в формуле F, представляющей функцию f все знаки функций заменить на знаки двойственных функций, то получится формула Пример. Получить функцию, двойственную к
Вывод: функция не самодвойственна. УПРАЖНЕНИЯ 1. Получить функцию, двойственную к
1) 2) 3) 4) 5)
2. Получить функцию, двойственную к
1) 2) 3) 4) 5) 3. Построить ДНФ двойственной функции, к функции, заданной своим вектор-столбцом.
4.Определить по вектор-столбцу, является ли функция самодвойственной. Если функция не самодвойственная, то а) построить ДНФ двойственной функции, к функции, заданной своим вектор-столбцом; б) по первой половине вектор-столбца функции доопределить самодвойственную функцию и выписать ее ДНФ.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 454. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
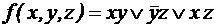 .
.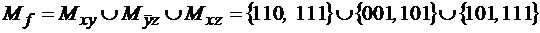 .
.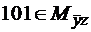 ( говорят, набор 101 покрывается множеством
( говорят, набор 101 покрывается множеством 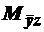 ), а
), а 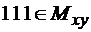 . Значит, если убрать из объединения составляющую
. Значит, если убрать из объединения составляющую 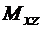 , объединение от этого не изменится. Говорят, что множество
, объединение от этого не изменится. Говорят, что множество 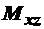 покрывается объединением
покрывается объединением 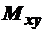 и
и 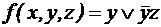 .
.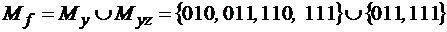 .
.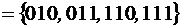 .
.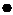
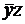
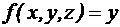 , и в данном случае является тупиковой, так как оставшийся импликант – простой.
, и в данном случае является тупиковой, так как оставшийся импликант – простой.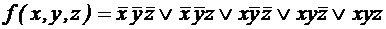 .
.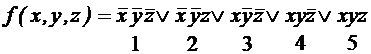 ;
;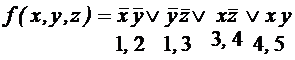 ;
;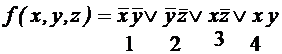 .
.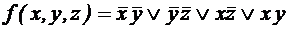 .
.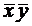
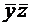
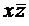
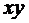
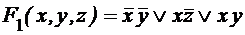 ;
;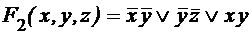 .
.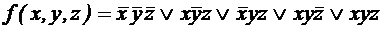
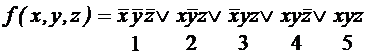 ;
;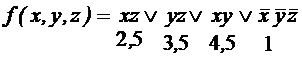 ;
;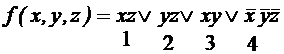 ;
;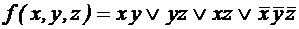 .
.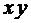
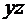
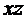
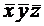
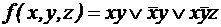 ;
;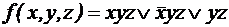 ;
;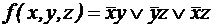 ;
;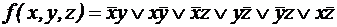 .
.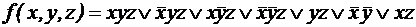
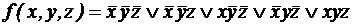 ;
; ;
;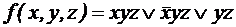 ;
;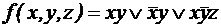
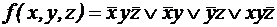 .
.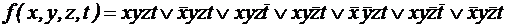 .
.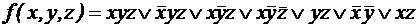
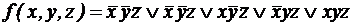 ;
;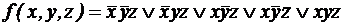 ;
;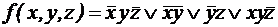 .
.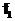
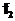
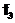
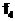
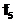
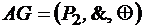 . В алгебре Жегалкина действуют тождества:
. В алгебре Жегалкина действуют тождества: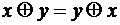 ;
;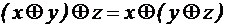 ;
;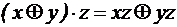 ,
,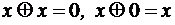
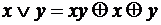 ,
,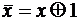 .
.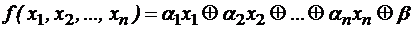 ,
,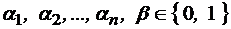 .
.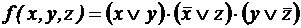 ;
;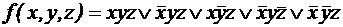 ;
;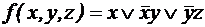 ;
; ;
;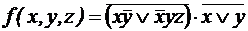 ;
;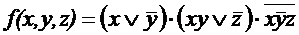 ;
; .
.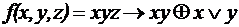 ;
;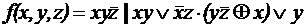 ;
;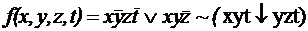 ;
;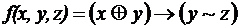 ;
;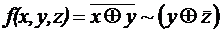 .
.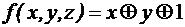 ;
; 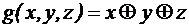 ;
; 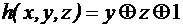 .
.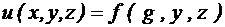 ; 2)
; 2) 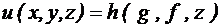 ;
;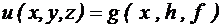 ; 4)
; 4) 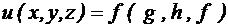 .
.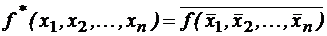 называется двойственнойфункцией к функции
называется двойственнойфункцией к функции 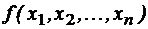 .
.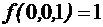 , то
, то 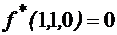 .
.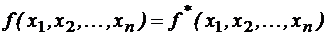 .
.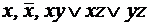 .
.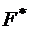 , представляющая функцию
, представляющая функцию 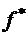 , двойственную к f.
, двойственную к f.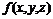 с помощью определения двойственной функции. Выяснить, является ли функция самодвойственной.
с помощью определения двойственной функции. Выяснить, является ли функция самодвойственной.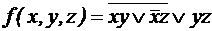
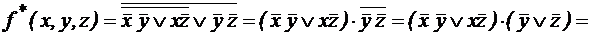
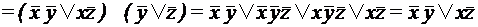 .
.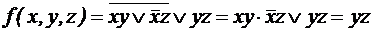 .
.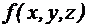 с помощью определения двойственной функции. Выяснить, является ли функция самодвойственной.
с помощью определения двойственной функции. Выяснить, является ли функция самодвойственной.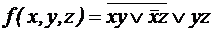 ;
;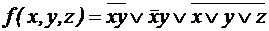 ;
;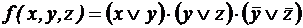 ;
;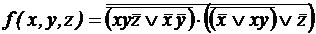
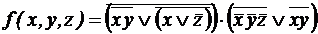 .
. ;
;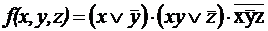 ;
;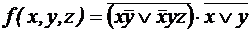 ;
;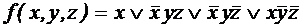 ;
;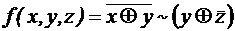 .
.