
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Эквивалентные преобразованияФормулы, представляющие одну и ту же функцию называются равносильными (эквивалентными). Булевыми операцияминазываются конъюнкция, дизъюнкция и отрицание. Булевой формулой называется формула, содержащая кроме символов переменных и скобок только символы конъюнкции, дизъюнкции и отрицания. Основные свойства булевых операций: 1) 3) 5) 7) 9) 11) 13) 14) 16) 18) Эти свойства проверяются путем подстановки в обе части равенства поочередно всех наборов значений аргументов. С помощью основных свойств булевых операций доказываются следующие законы: – закон поглощения 1) – закон простого склеивания
– закон расщепления
– закон обобщенного склеивания 1) Основные свойства булевых операций и законы применяются для эквивалентных преобразований одной равносильной формулы в другую.
Правило получения СДНФ из вектор-столбца 1. Выбрать все единичные наборы значений аргументов. 2. Каждому единичному набору поставить в соответствие элементарную конъюнкцию всех переменных так, чтобы в конъюнкции переменная была с отрицанием, если в наборе она равна 0. 3. Соединить полученные элементарные конъюнкции знаком дизъюнкции. 
УПРАЖНЕНИЯ Повторение 1. Упростить формулу 1) 2) 3)
2. Разложить функцию по переменной х; у; z. 1) 2) 3)
3. Упростить формулу 1) 2) 3) 4) 5) 6) 7) 8)
4. Привести ДНФ к СДНФ путем расщепления. 1) 2) 3) 4)
Дизъюнктивные и конъюнктивные нормальные формы Правило перехода от ДНФ к КНФ 1. Пусть дана ДНФ F функции f.
Здесь 2. Применим закон двойного отрицания: 3. Приведем к ДНФ
Здесь 4. Возьмем второе отрицание над F. Во время преобразования не будем раскрывать скобки – остановимся на формуле, имеющей вид конъюнкции элементарных дизъюнкций – КНФ.
Замечание. Если при приведении к ДНФ
Правило получения СКНФ из вектор-столбца 1. Выбрать все нулевые наборы значений аргументов. 2. Каждому нулевому набору поставить в соответствие элементарную дизъюнкцию всех переменных так, чтобы в дизъюнкции переменная была с отрицанием, если в наборе она равна 1. 3. Соединить полученные элементарные дизъюнкции знаком конъюнкции. УПРАЖНЕНИЯ Повторение 1. Упростить формулу 1) 2) 3)
2. Разложить функцию по переменной х; у; z. 1) 2) 3)
3. Перейти от ДНФ 1) 2) 3) 4) 5) 6) 4. Построить СКНФ с помощью вектор-столбца. 1) 2) 3) 4) Дизъюнктивные нормальные формы и импликанты Функция f имплицирует функцию g, если Замечание: Если Если f имплицирует g, и f представлена единственной элементарной конъюнкцией, то f называется импликантом g. Если из импликанта нельзя удалить ни одной переменной, то оно называется простым импликантом. Теорема Если функция – всех n переменных, то – Пример. Пусть Пусть Утверждение 1. Представление функции в виде ДНФ соответствует представлению ее единичного множества в виде объединения единичных множеств входящих в эту ДНФ элементарных конъюнкций. Пример. Пусть функция представлена своей ДНФ.
Тогда ее единичное множество может быть представлено в виде:
Получилось, что Утверждение 2. Любая конъюнкция ДНФ функции является импликантом данной функции. Утверждение 3. Если конъюнкция ДНФ функции не является простым импликантом, то можно найти соответствующий ей простой импликант (импликанты) и заменить им (их дизъюнкцией) непростой импликант. ДНФ, состоящая только из простых импликантов, называется сокращенной. Пример. Пусть функция представлена своей ДНФ.
Тогда ее единичное множество имеет вид:
Очевидно, что Проверим, будет ли простым импликант Вычеркнем из него переменную х. Получим конъюнкцию В свою очередь, полученный импликант Значит, импликант Вычеркнем из k переменную Вычеркнем из него переменную z. Получим конъюнкцию Таким образом, ДНФ вида УПРАЖНЕНИЯ 1. Проверить, будет ли функция f имплицировать функцию g. 1) 2) 3) 4)
2. Проверить, будут ли для функции 1) 2) 3)
3. Проверить, будут ли простыми импликантами конъюнкции следующей ДНФ. Получить сокращенную ДНФ, заменив непростые импликанты простыми,: 1) 2) 3) 4)
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 708. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ; 6)
; 6)  ;
; ; 8)
; 8)  ;
; ; 10)
; 10)  ;
; ; 12)
; 12)  ;
; ;
; ; 15)
; 15) 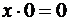 ;
; ; 17)
; 17)  ;
;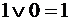 ; 19)
; 19)  .
. ; 2)
; 2)  ;
; ;
; ;
; ; 2)
; 2)  .
. с помощью эквивалентных преобразований. Получить дизъюнктивную нормальную форму (ДНФ). Привести формулу к СДНФ путем расщепления.
с помощью эквивалентных преобразований. Получить дизъюнктивную нормальную форму (ДНФ). Привести формулу к СДНФ путем расщепления. ;
; ;
; .
.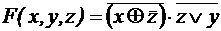 ;
; ;
; .
. с помощью эквивалентных преобразований. Получить дизъюнктивную нормальную форму (ДНФ). Построить СДНФ из вектор-столбца.
с помощью эквивалентных преобразований. Получить дизъюнктивную нормальную форму (ДНФ). Построить СДНФ из вектор-столбца. ;
; ;
; ;
; ;
; ;
; ;
; ;
;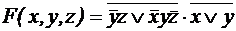 .
. ;
; ;
; ;
; .
. .
. – элементарные конъюнкции.
– элементарные конъюнкции. .
. .
.


 – элементарные дизъюнкции.
– элементарные дизъюнкции.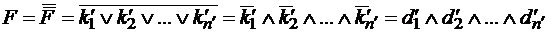
 ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
;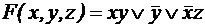 ;
;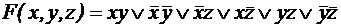 ;
; .
. .
. .
. представима единственной элементарной конъюнкцией
представима единственной элементарной конъюнкцией ;
;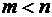 переменных, то
переменных, то  .
. . Она принимает значение 1 тогда и только тогда, когда x = 1, y = 1, z = 1. Значит
. Она принимает значение 1 тогда и только тогда, когда x = 1, y = 1, z = 1. Значит  .
.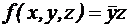 . Она принимает значение 1 тогда и только тогда, когда y = 0, z = 1. Значит, чему равняется переменная х – неважно, и она может принимать любые значения. Поэтому
. Она принимает значение 1 тогда и только тогда, когда y = 0, z = 1. Значит, чему равняется переменная х – неважно, и она может принимать любые значения. Поэтому  .
.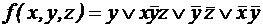 .
.
 .
. .
. .
.
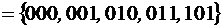 .
.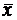 – это простой импликант. Он состоит из одной буквы, и если ее вычеркнуть, получится вырожденная конъюнкция (конъюнкция не имеющая переменных), что возможно только в случае, если
– это простой импликант. Он состоит из одной буквы, и если ее вычеркнуть, получится вырожденная конъюнкция (конъюнкция не имеющая переменных), что возможно только в случае, если  .
. . Ее единичное множество содержит 2 набора:
. Ее единичное множество содержит 2 набора: 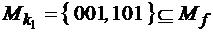 , то есть
, то есть  по-прежнему является импликантом f. Значит
по-прежнему является импликантом f. Значит  – так как оставшаяся переменная z имеет единичное множество, содержащее 4 вектора с последней 1, а в
– так как оставшаяся переменная z имеет единичное множество, содержащее 4 вектора с последней 1, а в  таких векторов только 3; z – так как оставшаяся переменная
таких векторов только 3; z – так как оставшаяся переменная  . Ее единичное множество содержит 2 набора:
. Ее единичное множество содержит 2 набора:  , то есть
, то есть  уже не является импликантом f.
уже не является импликантом f.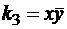 . Ее единичное множество содержит 2 набора:
. Ее единичное множество содержит 2 набора:  , то есть
, то есть  также не является импликантом f.
также не является импликантом f. является сокращенной.
является сокращенной. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. импликантами конъюнкции
импликантами конъюнкции  и
и  ;
;  ;
;  .
. ;
;  ;
;  .
. ;
;  ;
;  .
. ;
; ;
; ;
; .
.