
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Функциональная полнота системФункционально полной называется такая система функций Например, Теорема. Произвольная система Это означает, что через функции системы Лемма 1. Если функция Лемма 2. Если функция Функционально полной в слабом смысле называется такая система функций Например, Теорема 1 о функциональной полноте. Для того чтобы система функций Лемма 3. Если функция Теорема 2 о функциональной полноте (теорема Поста). Для того чтобы система функций хотя бы одну немонотонную, хотя бы одну нелинейную,  хотя бы одну несамодвойственную, хотя бы одну не сохраняющую 0, хотя бы одну не сохраняющую 1 функцию. УПРАЖНЕНИЯ 1. Проверить монотонность функции, используя определение. 1) 2) 3) 4) 5) 2. Проверить монотонность функции, используя теорему о булевой формуле монотонной функции. 1) 2) 3) 4) 5) 3. С помощью немонотонной функции и подстановки констант получить отрицание, используя лемму 1. 1) 2) 4. С помощью нелинейной функции и отрицания подстановкой констант получить дизъюнкцию или конъюнкцию, используя лемму 1 1) 2) 3) 5. Проверить функциональную полноту системы логических функций. Построить таблицу Поста, сделать вывод. 1) 2) 6. Привести выражение к формуле, выраженной через функционально полную систему 1) 2) 3) 4) 7. Система состоит из одной логической функции, заданной своим вектор-столбцом. Построить таблицу Поста и сделать вывод о функциональной полноте данной системы. 1) 2) 3) 4)
ГЛАВА 5. ЛОГИКА ВЫСКАЗЫВАНИЙ И ЛОГИКА ПРЕДИКАТОВ Логика высказываний Высказывание – это утверждение или повествовательное предложение, которое может быть либо истинным, либо ложным. Значением истинного высказывания является «И» – истина, ложного – «ложь». Повелительные («Войдите, пожалуйста»), вопросительные («Который час?») и бессмысленные предложения («Сумма пяти и восемнадцати»), в которых ничего не утверждается, не являются высказываниями. Предметом логики является анализ различных логических связей и методы построения на их основе правильных логических рассуждений. Способы построения новых высказываний из заданных с помощью логических связок и способы установления истинности высказываний, построенных таким образом, изучаются в логике высказываний. Основные логические связки - это связки: и, или, не, если … то…, которые в логике высказываний имеют специальные названия и обозначения. Иногда к ним добавляют еще две связки либо …, либо …(или …, или …); если, и только если (тогда и только тогда). Для одной и той же связки в разных источниках используются разные названия и обозначения, которые приведены в таблице 1. Таблица 1
В последней колонке табл. 1 записаны формулы, или выражения логики высказываний. С помощью букв А, В, С, ... обозначающих высказывания, связок и скобок можно построить разнообразные формулы. Исследование свойств таких формул и способов установления их истинности и является основным предметом логики высказываний. Существуют два подхода к построению логики высказываний, которые образуют два варианта этой логики: алгебру логики и исчисление высказываний. Алгебра логики Алгебра логики рассматривает логические формулы как алгебраические выражения, которые можно преобразовать по определенным правилам. Знаки операций обозначают логические операции (логические связки). В формулах алгебры логики переменные – это высказывания. Они принимают только два значения – ложь и истина, которые обозначаются либо 0 и 1, либо Л и И, либо false и true. Каждая формула задает логическую функцию: функцию от логических переменных, которая сама может принимать только два логических значения. Таблица функций
Таблица функций двух переменных
Значение любой логической формулы, содержащей знаки этих функций, на заданном наборе значений переменных можно вычислить, используя эти таблицы. Интерпретацией формулы логики высказываний называется набор значений высказываний, входящих в нее. Формула F называется тождественно истинной или тавтологией, если она принимает значение «истина» независимо от значений входящих в нее высказывательных переменных.Формула F называется выполнимой, если при некоторых значениях ее высказывательных переменных она принимает значение «истина». Такой набор значений высказывательных переменных называется моделью формулы F. Исчисление высказываний Пусть интерпретация Пусть Утверждение того, что некоторое высказывание (заключение) следует из других высказываний (посылок), называется аргументом. Аргумент часто представляют в виде:
... гипотезы
Аргумент называется правильным, если из множества гипотез логически следует заключение аргумента. Второе правило исчисления высказываний: Modus Ponens. Правило Modus Ponens: «Если
УПРАЖНЕНИЯ 1. Приведите примеры истинных и ложных высказываний из биологии, географии, физики, истории, математики, литературы. 2. Из данных предложений выберите те, которые являются высказываниями, обоснуйте выбор. 1) Коля спросил: «Который час»? 2) Как пройти в библиотеку? 3) Картины Пикассо слишком абстрактны. 4) Решение задачи – информационный процесс. 5) Число 2 является делителем числа 7 в некоторой системе счисления. 3. Выберите истинные из данных высказываний: 1) Город Лондон – столица Великобритании. 2) Число 3 является делителем числа 9. 3) Город Стокгольм – столица Германии. 4) Клавиатура – средство ввода информации. 5) Число 8 кратно 3. 6) Принтер – средство вывода информации. 7) Меню в программе – список возможных вариантов. 8) Для всех х из области определения 9) II+VI > VIII. 4. В приведенных предложениях вместо многоточия поставьте подходящие по смыслу слова: «необходимо», «достаточно», «необходимо и достаточно». Обозначив часть предложения до многоточия за А, а часть после многоточия за В, записать формализованное высказывание, используя подходящую логическую связку. 1) Для того, чтобы число делилось на 4, ... чтобы оно было четным. 2) Что бы число делилось на 3, ... что оно делилось на 9. 3) Для того чтобы число делилось на 10, ... чтобы оно оканчивалось на 0. 4) Чтобы произведение двух чисел равнялось 0, ... чтобы каждое из них равнялось 0. 5) Чтобы произведение двух чисел равнялось 0, ... чтобы хоть одно из них равнялось 0. 6) Чтобы умножить сумму нескольких чисел на какое-либо число, ... каждое слагаемое умножить на это число и полученные произведения сложить. 7) Чтобы произведение нескольких чисел разделить на какое-либо число, ... разделить на это число только один сомножитель, и полученное частное умножить на остальные сомножители. 8) Для того, чтобы сумма двух чисел была четной, ... чтоб каждое из них было четным числом. 9) Для того, чтобы число делилось на 10, ... чтобы оно делилось на 5. 10) Для того, чтобы число делилось на 6, ... чтобы оно делилось на 2 и на 3. 11) Для того, чтобы число делилось на 12, ... чтобы оно делилось на 2 и на 3. 12) Чтобы четырехугольник был квадратом, ... чтоб все его стороны были равны. 5. Формализовать сложное высказывание: разбить его на простые высказывания и связать их подходящими логическими связками. 1) Число 376 четное и трехзначное. 2) Зимой дети катаются на коньках или лыжах. 3) Новый год мы встретим на даче или на Красной площади. 4) Неверно, что Солнце движется вокруг Земли. 5) Если сейчас не солнечно, то пасмурно. 6) Земля имеет форму шара, который из космоса кажется голубым. 7) На уроке математики старшеклассники отвечали на вопросы учителя, а также писали самостоятельную работу. 8) Если вчера было воскресенье, то Дима не был в школе и весь день гулял. 9) Если сумма цифр натурального числа делится на 3, то и число делится на 3. 10) Число делится на 15 тогда и только тогда, когда оно делится на 3 и на 5. 6. Постройте отрицание следующих выражений. 1) Сегодня в театре идет опера «Евгений Онегин». 2) Число 2 есть простое число. 3) Число 3 – составное. 4) Каждый охотник желает знать, где сидит фазан. 5) Натуральные числа, оканчивающиеся на 0, являются простыми. 6) Неверно, что число 3 не является делителем числа 198. 7) Коля решил все задачи контрольной работы. 8) Неверно, что любое число, оканчивающееся на 4 делится на 4. 9) Во всякой школе некоторые ученики интересуются спортом. 10) Некоторые млекопитающие не живут на суше. 7. Являются ли отрицанием друг друга высказывания А и В. 1) А – «он мой друг»; В – «он мой враг». 2) А – «дом большой»; В – «дом небольшой». 3) А – « х > 2 »; В – « х < 2 ». 4) А – «две карты красные»; В – «две карты черные». 5) А – «две карты разные»; В – «две карты одинаковые». 6) А – «студент - девушка»; В – «студент - юноша». 7) А – «число четное»; В – «число нечетное». 8) А – «число положительное»; В – «число отрицательное». 9) А – «студент курит и живет в общежитии»; В – «студент не курит и не живет в общежитии». 10) А – « х ≤ 3»; В – « х > 3 ». 11) А – « 12) А – « 13) А – « 8. А – «Число 5 простое»; В – «Луна – спутник Венеры». Выразить обычным языком составные высказывания. Определите их истинность.
9. Какие из составных высказываний истинные. 1) У розы шипы и трава зеленая. 2) У розы шипы или трава красная. 3) Если у розы шипы, то трава красная. 4) Если трава красная, то у розы шипы. 5) Если трава синяя, то Земли спутник Луны. 6) Земля спутник Луны тогда и только тогда, когда трава красная. 7) Земля спутник Луны или Луна спутник Земли. 8) Неверно, что Земля спутник Луны и у розы шипы. 10. Для высказываний А и В определить истинность с семантический смысл и истинность составного высказывания: 1) A – Иван водит машину (истинно); В – мы без проблем доберемся до дома.
2) A – Лариса любит гонять на мотоцикле; В – быстро ездить опасно; С – жизнь Ларисы в опасности.
11. Являются ли следующие формулы выполнимыми Тождественно истинными Перечислить множество всех моделей формулы F. 1) 2) 12. Выполнимо ли множество формул: 1) 2) 13. Верно ли, что 1) 2) 14. Выяснить, являются ли следующие рассуждения логически правильными. Для этого представить каждое предложение в виде формулы и проверить, является ли заключение логическим следствием посылок. 1) Если Джон – коммунист, то Джон – атеист. Джон – атеист. Следовательно, Джон – коммунист. 2) Если этот курс хорош, то он полезен. Или экзаменатор снисходителен, или этот курс бесполезен. Но экзаменатор не снисходителен. Следовательно, этот курс плох. 3) Для того, чтобы перейти на следующий курс, достаточно сдать этот предмет по крайней мере на 3. Я сдам этот предмет лишь в том случае, если разберусь с доказательством теоремы. Но я не в состоянии разобрать доказательство этой теоремы. Следовательно, я перейду на следующий курс. 15. Определить, какие из следующих аргументов являются правильными: 1) Логика предикатов С помощью формул логики высказываний можно описать структуру сложных высказываний. Для описания внутренней логической структуры простых высказываний (т.е. высказываний, не содержащих связок) используются другие средства, которые вместе с логикой высказываний образуют логику предикатов. Чтобы яснее представить о какой логической структуре идет речь, рассмотрим пять высказываний: 1. 15 – нечетное число. 2. 8 – нечетное число. 3. 6 4. В Ярославле жителей больше, чем в Вязьме. 5. В Москве жителей больше, чем в любом другом городе России. Все эти высказывания – простые и, следовательно, в логике высказываний изображаются одной буквой. Все, что о них можно сказать в этой логике, – это то, что высказывание (2) ложно, а остальные – истинны. В то же время ясно, что между высказываниями (1) и (2) или между (4) и (5) сходства гораздо больше, чем между (1) и (5). В высказываниях (1) и (2) речь идет о числах, которым приписывается одно и то же свойство – нечетность. В высказывании (3) утверждается наличие отношения неравенства между числами. В высказываниях (4) и (5) говорится о городах, относительно которых утверждается наличие некоторого отношения между ними – «иметь больше жителей». Числа и города – это объекты. Множество объектов (целых чисел, городов России и т.д.), о которых делаются утверждения, называется предметной областью, а сами утверждения об отношениях между С математической точки зрения: n-местный предикат – это функция Нечетность – это одноместный предикат. Если его обозначить через «Иметь больше жителей» – это двуместный предикат Неравенство – тоже двуместный предикат, для обозначения которого можно сохранить обычную запись: Таким образом, формулы вида Кроме того, из предикатов можно получать конкретные высказывания, не содержащие предметных констант, а утверждающих нечто обо всей предметной области. В естественном языке это делается с помощью оборотов «для всех В языке формул логики предикатов этим оборотам соответствуют специальные знаки – кванторы: квантор общности Присоединение квантора с переменной Например, формула Если квантор навешивается на формулу с несколькими предметными переменными, то он уменьшает число свободных (несвязанных) переменных в этой формуле. Например, формула
в которой оба вхождения переменной Как и в логике высказываний, в логике предикатов имеются эквивалентные соотношения, позволяющие преобразовывать предикатные формулы. Например, - один квантор можно выразить через другой:
- формулу, не содержащую переменную
Однако, в целом, логику предикатов не удается представить в виде алгебры, столь же эффективной как алгебра логики (т.к. вычисление истинности предикатов, содержащих кванторы, в общем случае заключается в подстановке всех возможных значений предметных переменных, которых может быть бесконечное множество). Поэтому логика предикатов организуется в виде исчисления предикатов, которое содержит аксиомы и правила вывода исчисления высказываний, а также дополнительные предикатные аксиомы и правила вывода. В качестве аксиом обычно принимаются две формулы:
где в этих правилах требуется, чтобы формула Пример. Рассмотрим известнейший силлогизм, на протяжении двух тысячелетий переходящий из одних ученых трудов в другие: Все люди смертны. Сократ – человек. . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 878. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , через функции которой можно выразить любую логическую функцию.
, через функции которой можно выразить любую логическую функцию.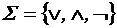 . Эта система функционально полна, так как любая функция имеет булеву формулу.
. Эта система функционально полна, так как любая функция имеет булеву формулу. будет функционально полной, если она сводится к функционально полной системе
будет функционально полной, если она сводится к функционально полной системе  – немонотонна, то подстановкой n-1 константы из нее можно получить отрицание.
– немонотонна, то подстановкой n-1 константы из нее можно получить отрицание. – функционально полна в слабом смысле. Эта система функций алгебры Жегалкина. Для того, чтоб с ее помощью можно было записать все полиномы Жегалкина, необходимо добавить константу 1. Это означает, что
– функционально полна в слабом смысле. Эта система функций алгебры Жегалкина. Для того, чтоб с ее помощью можно было записать все полиномы Жегалкина, необходимо добавить константу 1. Это означает, что  – функционально полна (в сильном смысле).
– функционально полна (в сильном смысле). ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
;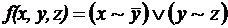 .
.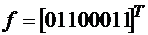 ; 3)
; 3)  ;
;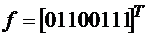 ; 4)
; 4)  .
. ;
; ;
; .
. ; 3)
; 3)  ; 5)
; 5)  ;
; ; 4)
; 4)  ; 6)
; 6)  .
. ,
,  ,
,  ,
,  :
:



 ; 5)
; 5) 
 ; 6)
; 6) 
 ; 7)
; 7)  .
. ;
;  , ØА
, ØА

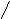 5. либо …,
либо …
5. либо …,
либо …
 одной переменной:
одной переменной:


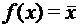

 , соответствующих основным логическим связкам:
, соответствующих основным логическим связкам:



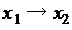



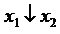
 определена на всех высказывательных переменных, встречающихся в формулах множества
определена на всех высказывательных переменных, встречающихся в формулах множества  . Говорят, что
. Говорят, что  из
из 


 заключение
заключение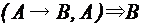 , т.е.
, т.е. , то
, то  ; но
; но  верно, что х+2 > 0.
верно, что х+2 > 0. »; В – «
»; В – «  ».
». »; В – «
»; В – «  ».
». »; В – «
»; В – «  ».
». ;
;
 ;
;
 ;
;
 ;
;
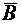 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
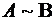 .
.
 .
. ;
;  .
.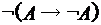 ; 3)
; 3)  ; 5)
; 5)  ;
;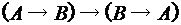 ; 4)
; 4)  ; 6)
; 6)  .
. ; 3)
; 3)  ;
;  ; 4)
; 4)  .
. ÷=
÷=  ; 3)
; 3)  ÷=
÷=  ÷=
÷= 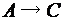 .
. 3)
3) 









 5.
5. объектами называются n-местными предикатами.
объектами называются n-местными предикатами. от
от  принимает два логических значения – истинно и ложно.
принимает два логических значения – истинно и ложно. , тогда высказывания (1) и (2) запишутся как
, тогда высказывания (1) и (2) запишутся как 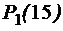 и
и  , т.е. как один и тот же предикат нечетности с разными значениями (15 и 8) переменной
, т.е. как один и тот же предикат нечетности с разными значениями (15 и 8) переменной  . Высказывание (4) можно записать как
. Высказывание (4) можно записать как  .
. .
. предметных констант – конкретных объектов из предметных областей.
предметных констант – конкретных объектов из предметных областей. и квантор существования
и квантор существования 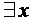 .
.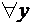
 ,
, ,
, 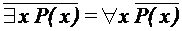 ,
, ;
; 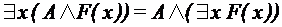 .
.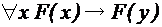 , (1)
, (1) , (2)
, (2) – любая предикатная формула, содержащая свободную переменную
– любая предикатная формула, содержащая свободную переменную  , (3)
, (3)  , (4)
, (4) содержала свободную переменную
содержала свободную переменную  ее не содержала.
ее не содержала.