
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные определения, способы задания,Основные классы, изоморфизм графов Графом (G) называется совокупность двух множеств: множества вершин (V) и множества ребер или дуг (E), между элементами которых определено отношение инцидентности. Вершина Вершины Ребра Граф, содержащий направленные ребра (дуги) с началом Граф, содержащий направленные ребра (дуги) называется, называется неориентированнымграфом (н-графом). Ребра (дуги), имеющие одинаковые концевые вершины, называются параллельными или кратными. Граф, содержащий кратные ребра, называется мультиграфом. Ребро, концевые вершины которого совпадают, называется петлей. Граф называется конечным, если множество его элементов (вершин и ребер) конечно. Нулевым, пустым (или полностью несвязным) графом называется граф с пустым множеством ребер (т.е. нулевой граф – это просто множество точек (вершин)). Простым графом называется граф без петель или кратных ребер. Полным графом называется (простой) граф, у которого каждая пара различных вершин связана ровно одним ребром. (Граф без кратных ребер называется полным, если каждая пара вершин в нем соединена ребром). Двудольным графом называется граф, у которого множество вершин имеет разбиение  Полным двудольным графом называется двудольный граф, у которого каждая вершина множества Дополнением графа G называется граф Каждому неориентированному графу канонически соответствует ориентированный граф с тем же множеством вершин, в котором каждое ребро заменено двумя ориентированными ребрами, инцидентными тем же вершинам и имеющим противоположные направления. Способы задания графа Задать граф – значит описать множества его вершин и ребер, а также отношение инцидентности. Для описания вершин и ребер достаточно их занумеровать. Пусть Отношение инцидентности задается: а) матрицей инцидентности для н-графа для ор-графа б) списком ребер графа, в котором каждая строка соответствует ребру и в ней записаны номера вершин графа, инцидентных этому ребру. Для н-графа порядок вершин в строке произволен, для ор-графа первым стоит номер вершины–начала ребра. в) матрицей смежности Вид матриц и списка ребер зависит от нумерации вершин и ребер графа. Граф считается полностью заданным, если нумерация его вершин зафиксирована. Графы, отличающиеся только нумерацией вершин, называются изоморфными. Перенумерация вершин и ребер графа задается соответственно строками Степени вершин графа (Локальной) Степенью или (валентностью) Если не оговаривается особо, то петля учитывается дважды при подсчете валентности вершины. Граф называется правильным (с валентностью r) или r-валентным графом (регулярным, однородным), если степени всех его вершин равны. Вершина называется изолированной, если она несмежна ни с одной из вершин графа, или, что то же самое, неинцидентна ни одному ребру. Степень этой вершины равна 0. Вершина, имеющая степень, равную 1, называется висячей (концевой). Ребро, инцидентное висячей вершине, называют концевым. Утверждение 1. (лемма о рукопожатиях): В н-графе сумма степеней всех вершин равна удвоенному числу ребер (т.е. четна): Следствие 1. Произвольный граф имеет четное число вершин нечетной степени. Следствие 1. Число ребер в полном графе равно В ор-графе две (локальных) степени вершины: Утверждение 2.Суммы степеней всех вершин ор-графа равны количеству ребер этого графа и, следовательно, равны между собой: Части, суграфы и подграфы Граф H называется частью графа G (
Если множества вершин части графа H и графа G совпадают: Подграфом (Подграф Операции над частями графа Дополнение
Сумма
Произведение
Части
Части
Если
Графы и бинарные отношения Отношению R, заданному на множестве V, взаимно однозначно соответствует ориентированный граф G(R) без кратных ребер с множеством вершин V, в котором ребро Граф G( Граф обратного отношения G( Граф объединения двух отношений, заданных на V,
Граф пересечения отношений на V,
УПРАЖНЕНИЯ 1. Для приведенных графов построить матрицу инцидентности и матрицу смежности. Найти степени вершин графа. Определить свойства отношения, которому соответствует граф.
Рис. 1 Рис. 2
2. Для приведенных графов построить матрицу инцидентности. Стереть рисунок. Найти степени вершин по матрице инцидентности.
Рис. 1 Рис. 2
3. Для приведенных графов построить матрицу смежности. Стереть рисунок. Найти степени вершин по матрице смежности.
Рис. 1 Рис.2
4. Дана матрица инцидентности графа. Задать граф рисунком. 1) 2) 3)
5. Дана матрица смежности неориентированного графа. Задать граф рисунком.
1) 2) 3)
6. Дана матрица смежности орграфа. Задать граф рисунком.
1) 2) 3)
7. Дана матрица смежности. Построить соответствующий ей неориентированный и ориентированный графы.
1) 2) 3)
8. Для графа G, приведенного на рисунке определить различные части графа:
Найти сумму Найти пересечение Найти дополнение до графа G частей
Рис. 1 Рис. 2
Рис. 3 Рис. 4 9. Для графа G, изображенного на рисунке: Определить, является ли следующая часть 1) 2) 3) 4) 5) Выполнить операции над
10. Изоморфны ли графы, изображенные на рисунке? Построить матрицы смежности изоморфных графов, определить их тип, соответствующие бинарные отношения и подсчитать сумму степеней вершин.
11. Показать, что два графа изоморфны. Построить матрицы смежности изоморфных графов, подсчитать сумму степеней вершин, определить тип графов и своства соответствующих им бинарных отношений. Указание: для проверки изоморфизма построить матрицы смежности. 1) 2) 12. Среди пар графов, изображенных на рисунке, указать пары изоморфных графов и пары неизоморфных графов. Ответ обосновать.
13. Задать различными способами, определенные ниже графы G. Определить их типы, построить дополнения
|
||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 385. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  инцидентны друг другу, если вершина является для этого ребра концевой точкой.
инцидентны друг другу, если вершина является для этого ребра концевой точкой. и
и  называются смежными, если существует ребро, соединяющее их, т.е. они инцидентны одному и тому же ребру.
называются смежными, если существует ребро, соединяющее их, т.е. они инцидентны одному и тому же ребру. и
и 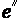 называются смежными, если они имеют, по крайней мере, одну общую вершину.
называются смежными, если они имеют, по крайней мере, одну общую вершину. и концом
и концом  такое, что каждое ребро связывает вершины из множества
такое, что каждое ребро связывает вершины из множества  с вершиной из множества
с вершиной из множества  . (Двудольным графом называется граф, множество вершин которого можно разбить на два непустых подмножества (на две доли)
. (Двудольным графом называется граф, множество вершин которого можно разбить на два непустых подмножества (на две доли)  с теми же вершинами, что и граф G, и содержащий только те ребра, которые нужно добавить к графу G, чтобы получился полный граф. (Дополнением графа G называется граф
с теми же вершинами, что и граф G, и содержащий только те ребра, которые нужно добавить к графу G, чтобы получился полный граф. (Дополнением графа G называется граф  вершины графа;
вершины графа;  ребра графа G.
ребра графа G. размера
размера  (строкам соответствуют ребра, столбцам – вершины графа), в которой
(строкам соответствуют ребра, столбцам – вершины графа), в которой

 размера
размера  , столбцам и строкам которой соответствуют вершины графа. Для н-графа
, столбцам и строкам которой соответствуют вершины графа. Для н-графа  равно количеству ребер, инцидентных i-й и j-й вершинам, для ор-графа
равно количеству ребер, инцидентных i-й и j-й вершинам, для ор-графа  и
и  новых номеров вершин и ребер, расположенных в исходном порядке.
новых номеров вершин и ребер, расположенных в исходном порядке. вершины называется число ребер, инцидентных вершине v.
вершины называется число ребер, инцидентных вершине v.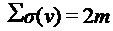 , где m – число ребер.
, где m – число ребер. , где n – число вершин.
, где n – число вершин. и
и  число ребер с началом и концом в v соответственно.
число ребер с началом и концом в v соответственно. , m – число ребер.
, m – число ребер.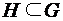 ), если множества его вершин и ребер содержатся в множествах вершин и ребер графа G:
), если множества его вершин и ребер содержатся в множествах вершин и ребер графа G:

 , то граф H называется суграфом графа G. Суграф H называется покрывающим для н-графа G, если любая вершина графа G инцидентна хотя бы одному ребру из Н. (Т.е., если граф G не имеет изолированных вершин, то и суграф покрывающий так же не должен иметь изолированных вершин).
, то граф H называется суграфом графа G. Суграф H называется покрывающим для н-графа G, если любая вершина графа G инцидентна хотя бы одному ребру из Н. (Т.е., если граф G не имеет изолированных вершин, то и суграф покрывающий так же не должен иметь изолированных вершин). графа
графа  с множеством вершин
с множеством вершин 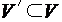 называется часть графа, которой принадлежат все ребра инцидентные
называется часть графа, которой принадлежат все ребра инцидентные 
 к части H определяется множеством всех ребер графа G, не принадлежащих H:
к части H определяется множеством всех ребер графа G, не принадлежащих H: ,
,  ;
;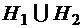 частей
частей  и
и  графа G, это граф, у которого
графа G, это граф, у которого и
и 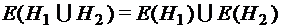 ;
; частей
частей  и
и  .
.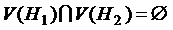 ,
,  .
. существует, только если выполнено
существует, только если выполнено  . Симметричному отношению R взаимно однозначно соответствует неориентированный граф без кратных ребер G(R). Антисимметричному отношению R взаимно однозначно соответствует ориентированный граф без кратных ребер, не содержащий пар вершин с ребрами, противоположно направленными к разным вершинам. Если R рефлексивно, то граф G(R) без кратных ребер имеет петли во всех вершинах. Если R антирефлексивно, то граф G(R) без кратных ребер не имеет петель. Если R транзитивно, то в графе G(R) без кратных ребер для каждой пары ребер
. Симметричному отношению R взаимно однозначно соответствует неориентированный граф без кратных ребер G(R). Антисимметричному отношению R взаимно однозначно соответствует ориентированный граф без кратных ребер, не содержащий пар вершин с ребрами, противоположно направленными к разным вершинам. Если R рефлексивно, то граф G(R) без кратных ребер имеет петли во всех вершинах. Если R антирефлексивно, то граф G(R) без кратных ребер не имеет петель. Если R транзитивно, то в графе G(R) без кратных ребер для каждой пары ребер  имеется замыкающее ребро
имеется замыкающее ребро  . Пусть
. Пусть  – дополнение отношения R на V:
– дополнение отношения R на V:  , где U –универсальное (полное) отношение
, где U –универсальное (полное) отношение  , т.е. отношение, имеющее место между любой парой элементов из V.
, т.е. отношение, имеющее место между любой парой элементов из V.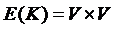 ).
). ) отличается от графа G(R) тем, что направления всех ребер заменены на обратные.
) отличается от графа G(R) тем, что направления всех ребер заменены на обратные. является графом суммы двух графов
является графом суммы двух графов  и
и 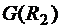 :
: .
.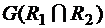 является графом пересечения двух графов
является графом пересечения двух графов  .
.
 .
.















 – суграф не покрывающий;
– суграф не покрывающий; – суграф покрывающий;
– суграф покрывающий; – подграф, порожденный множеством вершин
– подграф, порожденный множеством вершин – звездный граф (для некоторой выбранной вершины);
– звездный граф (для некоторой выбранной вершины);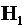 и
и 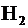 , будет ли эта сумма прямой?
, будет ли эта сумма прямой? и
и  .
. .
.
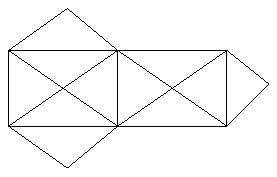


 (
(  ) графа G подграфом, суграфом, покрывающим суграфом, если:
) графа G подграфом, суграфом, покрывающим суграфом, если: ,
,  ;
;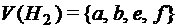 ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
, 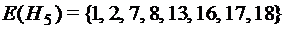 .
. ,
,  .
.




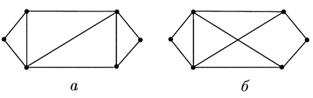
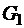 – треугольник;
– треугольник;  – четырехугольник;
– четырехугольник; 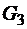 – пятиугольник.
– пятиугольник.