
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Полугруппы, группы, решеткиАлгебра с одной бинарной ассоциативной операцией называется полугруппой. Эта операция обычно называется умножением и обозначается Пример 1. Множество действительных чисел с операцией умножения является полугруппой с единицей. Здесь е = 1. Утверждение 1. Единица в полугруппе всегда единственна. Группой называется полугруппа с единицей, в которой для каждого элемента а существует обратный элемент Утверждение 2. Для каждого элемента а в группе существует единственный обратный элемент Число элементов группы называется порядком группы. Группа называется абелевой, если операция группы коммутативна. Группа, все элементы которой является степенями одного и того же элемента а, называется циклической. Утверждение 3. Циклическая группа всегда абелева. Пример 2. Множество целых чисел с операцией сложения является циклической. Пример 3. Множество целых чисел с операцией сложения является абелевой группой. Единицей по сложению является Множество, на котором кроме операций заданы отношения называется алгебраической системой. Таким образом, алгебра является частным случаем алгебраической системы.  Рассмотрим частный случай алгебраической системы – решетку. Пусть дано частично-упорядоченное множество М. Отношение порядка в общем случае будем обозначать Решеткой называется частично упорядоченной множество, в котором для любых двух элементов а и b существует и единственна наибольшая нижняя грань, обозначаемая Пример 4. Любое полностью упорядоченное множество (например, множество целых чисел) можно превратить в решетку, определив для любых а и b из М УПРАЖНЕНИЯ 1. Проверить коммутативность и ассоциативность операций. 1) сложение чисел; 2) умножение чисел; 3) сложение матриц; 4) умножение матриц (проверить на примере квадратных матриц А, В и С 2-ого порядка); 5) возведение в степень; 6) ln xy (где х, у >0); 7) х-у; з) х/у. 2.Проверить дистрибутивность слева и справа операции ψ отношению к операции φ. 1) φ – сложение чисел, ψ – умножение чисел; 2) φ – умножение чисел, ψ – сложение чисел; 3) φ – объединение множеств, ψ – пересечение множеств; 4) φ – пересечение множеств, ψ – объединение множеств; 5) φ – умножение чисел, ψ – возведение в степень; 6) φ – возведение в степень, ψ – умножение чисел; 7) φ – возведение в степень, ψ – сложение чисел. 3. На множестве 4. На множестве Найти значения выражений: 1) 2) 5. В конечной алгебре поля 1) 2) 6. В поле
1) единичный элемент по операции * ; 2) единичный элемент по операции + ; 3) противоположный и обратный элемент для каждого элемента 4) найти значения выражений: а) б) в) 5) решить систему 7. Дано множество
Найти единичные элементы по операциям
8. Доказать единственность единичного элемента в группе. 9. Доказать единственность обратного элемента в группе. 10. Пусть 11. Дано Проверить, будет ли алгебра 12. Составить полугруппу с операцией Что надо сделать, чтобы эта полугруппа стала моноидом. 13. Пусть S – множество всех перестановок 14. Будет ли алгебра (B (U), 15. Будет ли алгебра ( 16. Является ли решеткой множество целых чисел Z с операциями
17. Будет ли решеткой множество, диаграмма Хасса которой изображена на рисунке. Почему?
Рис. 1 Рис. 2 Рис. 3
18. Проверить на примере выполнение условия изоморфизма между алгебрами: 1) (B (U), 2) ( 19. Определить изоморфны ли алгебры: 1) 2) 3) 4) 5) 6) 7) ГЛАВА 2. ТЕОРИЯ ГРАФОВ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 320. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 или ab. Такая запись называется мультипликативной. В частности аа обозначается как
или ab. Такая запись называется мультипликативной. В частности аа обозначается как  , ааа как
, ааа как  и т. д. В общем случае
и т. д. В общем случае  . Полугруппа называется коммутативной, если операция умножения коммутативна. Если полугруппа содержит такой элемент е, что для любого а выполняется
. Полугруппа называется коммутативной, если операция умножения коммутативна. Если полугруппа содержит такой элемент е, что для любого а выполняется  , то такой элемент называется единицей. Полугруппа с единицей называется моноидом.
, то такой элемент называется единицей. Полугруппа с единицей называется моноидом. , удовлетворяющий условию
, удовлетворяющий условию  .
. . Для каждого числа
. Для каждого числа 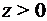 существует обратный (здесь: противоположный) – z < 0. И наоборот. Для числа 0 противоположным является число 0.
существует обратный (здесь: противоположный) – z < 0. И наоборот. Для числа 0 противоположным является число 0. . Верхней гранью элементов а и b из М называется элемент
. Верхней гранью элементов а и b из М называется элемент  , такой что
, такой что  и
и  . Нижней граньюэлементов а и b из М называется элемент
. Нижней граньюэлементов а и b из М называется элемент  , такой что
, такой что  и
и  . В общем случае для некоторых элементов а и b нижняя грань может не существовать или не быть единственной.
. В общем случае для некоторых элементов а и b нижняя грань может не существовать или не быть единственной. и наименьшая верхняя грань, обозначаемая
и наименьшая верхняя грань, обозначаемая  . Таким образом решетка – это алгебраическая система вида
. Таким образом решетка – это алгебраическая система вида  с одним бинарным отношением и одной бинарной операцией.
с одним бинарным отношением и одной бинарной операцией. ;
;  .
. задать с помощью таблицы Келли операции
задать с помощью таблицы Келли операции  – сложение по модулю 4 и
– сложение по модулю 4 и  – умножение по модулю 4. Продемонстрировать на примере их коммутативность, ассоциативность, дистрибутивность
– умножение по модулю 4. Продемонстрировать на примере их коммутативность, ассоциативность, дистрибутивность 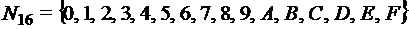 задать с помощью таблицы Келли операции
задать с помощью таблицы Келли операции  ;
;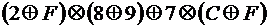 .
. рассчитать значения выражений:
рассчитать значения выражений: ;
;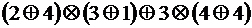 .
. , операции которого заданы таблицами Келли
, операции которого заданы таблицами Келли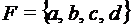 ;
; ;
;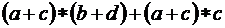 ;
; .
. ;
; .
.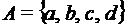 . Задано поле
. Задано поле  , где
, где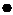
 ;
; .
. – ассоциативная операция, заданная на множестве А, такая что для каждого элемента
– ассоциативная операция, заданная на множестве А, такая что для каждого элемента  существует обратный элемент
существует обратный элемент  . Доказать, что
. Доказать, что 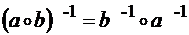 .
. . На множестве А заданы преобразования
. На множестве А заданы преобразования  . На множестве преобразований
. На множестве преобразований  задана операция композиции преобразований
задана операция композиции преобразований  полугруппой.
полугруппой.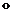 – композиция преобразований, для которой множество подстановок
– композиция преобразований, для которой множество подстановок 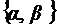 является системой образующих.
является системой образующих. . Определить свойства алгебры
. Определить свойства алгебры  . Будет ли оно группой? Будет ли группа абелевой?
. Будет ли оно группой? Будет ли группа абелевой? ) решеткой? Изобразить диаграмму Хасса.
) решеткой? Изобразить диаграмму Хасса. ) решеткой? Изобразить диаграмму Хасса.
) решеткой? Изобразить диаграмму Хасса. и
и  , таких что для любых
, таких что для любых 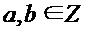 выполняется:
выполняется: ,
,  .
.


 , ┐) и (
, ┐) и (  , ┐);
, ┐); , ┐); (B (U),
, ┐); (B (U),  , ┐) , где
, ┐) , где  .
. и
и  , где гомоморфизм задается
, где гомоморфизм задается  ;
; , где гомоморфизм задается
, где гомоморфизм задается  ;
; и
и 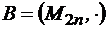 , где гомоморфизм задается
, где гомоморфизм задается  и
и  , где гомоморфизм задается
, где гомоморфизм задается 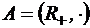 и
и  , где гомоморфизм задается
, где гомоморфизм задается  ;
; и
и  , где гомоморфизм задается
, где гомоморфизм задается 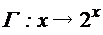 .
.