
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ГЛАВА 4. АЛГЕБРА ЛОГИЧЕСКИХ ФУНКЦИЙОсновные определения Двоичное (бинарное) множество Логической функцией называется операция типа Утверждение:
Единичным набором значений аргументов называется набор, на котором функция равна 1. Множество единичных наборовфункции f называется единичным множеством – Нулевым набором значений аргументов называется набор, на котором функция равна 0. Множество нулевых наборовфункции f называется нулевым множеством –
Таблица логических функций одной переменной
Таблица логических функций двух переменных
Функции № 0 и № 15 – функции константы 0 и 1. Константы принимают одно и то же значение при любых наборах значений аргументов. Функция № 1 – конъюнкция x и y. Обозначение конъюнкции Функция № 7 – дизъюнкция x и y. Обозначение дизъюнкции  Функция № 9 – эквивалентность x и y. Обозначение эквивалентности Функция № 6 – сложение по модулю 2 x и y. Обозначение сложения по модулю 2 Функция № 13 – импликация x и y. Обозначение импликации Функция № 11 – импликация у и х. Обозначение – Функция № 14 – штрих Шеффера x и y. Обозначение штриха Шеффера Функция № 8 – стрелка Пирса x и y. Обозначение стрелки Пирса Введем обозначения:
Теорема о разложении функции по переменным Всякая логическая функция
Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций. Дизъюнктивная форма будет совершенной (СДНФ), если каждая элементарная конъюнкция содержит все наименования переменных. Элементарной дизъюнкцией называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза. Конъюнктивная нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций. Конъюнктивная форма будет совершенной (СКНФ), если каждая элементарная дизъюнкция содержит все наименования переменных. УПРАЖНЕНИЯ 1. Записать вектор-столбец функции, заданной формулой: 1) 2) 3) 4) 5) 6) 7) 2. Разложить 1) по переменной х функцию 2) по переменной у функцию 3) по переменной z функцию 4) по переменным х и у функцию 5) по переменным х и z функцию 6) по переменным у и z функцию 7) по переменным х, у и z функцию Вывести правило получения совершенной дизъюнктивной нормальной формы из вектор-столбца. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 305. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , где логический символ 0 означает – «ложь», логический символ 1 означает – «истина».
, где логический символ 0 означает – «ложь», логический символ 1 означает – «истина». .
.  – множество всех логических функций от n переменных.
– множество всех логических функций от n переменных.  – множество всех логических функций.
– множество всех логических функций. .
. .
. .
.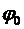



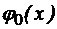 = 0 – функция-константа 0;
= 0 – функция-константа 0; – тождество переменной х;
– тождество переменной х; – отрицание переменной х;
– отрицание переменной х;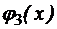 = 1 – функция-константа 1.
= 1 – функция-константа 1. . Конъюнкция принимает значение 1 только в случае, когда и х и у равны 1.
. Конъюнкция принимает значение 1 только в случае, когда и х и у равны 1. . Дизъюнкция принимает значение 1 тогда, когда х или у равны 1 (т.е. хотя бы один аргумент).
. Дизъюнкция принимает значение 1 тогда, когда х или у равны 1 (т.е. хотя бы один аргумент). . Эквивалентность принимает значение 1 только в случае, когда х и у равны.
. Эквивалентность принимает значение 1 только в случае, когда х и у равны. . Сложение по модулю 2 принимает значение 1 только в случае, когда сумма х и у нечетна.
. Сложение по модулю 2 принимает значение 1 только в случае, когда сумма х и у нечетна. . Импликация принимает значение 0 только в случае, когда из «истины» следует «ложь».
. Импликация принимает значение 0 только в случае, когда из «истины» следует «ложь». .
.  . Штрих Шеффера является отрицанием конъюнкции:
. Штрих Шеффера является отрицанием конъюнкции: 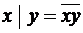 .
.  . Стрелка Пирса является отрицанием дизъюнкции:
. Стрелка Пирса является отрицанием дизъюнкции: 
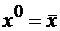 ;
;  .
. может быть разложена по переменным
может быть разложена по переменным  , где
, где 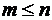 , то есть представлена в виде:
, то есть представлена в виде: Дизъюнкция в правой части равенства берется по всем наборам параметров
Дизъюнкция в правой части равенства берется по всем наборам параметров  . Конъюнкций, соединенных знаком дизъюнкции будет
. Конъюнкций, соединенных знаком дизъюнкции будет  штук.
штук. Разложение функции по всем переменным носит название совершенной дизъюнктивной нормальной формы.
Разложение функции по всем переменным носит название совершенной дизъюнктивной нормальной формы. ;
;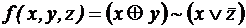 ;
; ;
; ;
; ;
; ;
;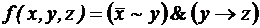 .
.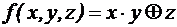 ;
; ;
;
 ;
; ;
;
 .
.