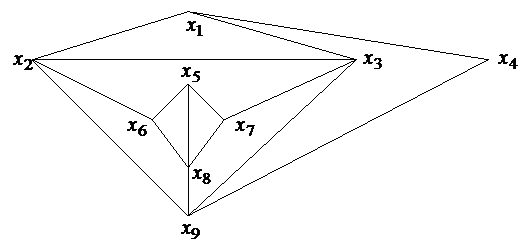Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Характеристические числа графов. СетиДерево – это связный ациклический граф. Теорема 1 Граф G является деревом тогда и только тогда, когда любые 2 его вершины связаны единственной простой цепью. Теорема 2 Граф G является деревом с n вершинами тогда и только тогда, когда у него ровно n-1 ребро. Лес из k деревьев – это несвязный ациклический граф, содержащий ровно k компонент связности. Теорема 3 Лес с n вершинами, состоящий из k деревьев, содержит ровно n-k ребер. Остов графа G– это подграф графа G, который является деревом. Концевая вершина дерева – вершина, локальная степень которой равна 1. Концевое ребро – ребро инцидентное концевой вершине. Пусть дано дерево Т. Назовем концевые вершины дерева Т вершинами типа 1. Удалим из дерева Т все концевые ребра. Получим дерево Т1. Его концевые вершины назовем вершинами типа 2 (для исходного дерева Т). Продолжаем процесс, пока не останутся вершины максимального типа. Их может быть 1 или 2. Теорема 4 Центрами деревьев являются вершины максимального типа и только они. Все диаметральные цепи проходят через центры и имеют длину 2k–2, если центр 1; 2k–2, если центра 2. Корнем дерева называется любая помеченная вершина. Если в дереве определен корень, все ребра графа можно ориентировать (от корня). Причем, ребро (a, b) ориентируется от a к b, если цепь, связывающая корень с вершиной а не проходит через вершину b, и наоборот. Ветвью вершины а называется подграф, порожденный множеством В(а) – вершин, связанных с корнем цепями, проходящими через вершину а. Характеристические числа графа – это цикломатическое число, число внутренней устойчивости и число внешней устойчивости.  Цикломатическое число графа G находится по формуле:
Здесь Теорема 5
Число внутренней устойчивости графа G обозначается Множеством внешней устойчивости графа G (внешне устойчивым множеством)называется любое множество вершин Q такое, что из каждой вершины множества Число внешней устойчивости графа G обозначается
Сетью называется любой частично-ориентированный граф S, некоторые вершины которого помечены. Некоторые помеченные вершины называются входными полюсами, другие – выходными полюсами. Непомеченные вершины называются внутренними. Простая цепь, связывающая входной и выходной полюс будет называться цепью. Если сеть содержит k входных и n выходных полюсов, то она называется (k, n)-полюсником. Двухполюснойсетью называется сеть, являющаяся (1, 1)-полюсником. Пусть дана частично ориентированная двухполюсная сеть. Пусть для каждого ребра сети определена пропускная способность ребра Потоком в сети называется пара объектов 1) ограничение:
2) для каждой внутренней вершины выполняется закон Киргоффа:
где где
Если
Величиной потока в сети назовем число Сечением в сети называется совокупность ребер, при удалении которых сеть становится несвязной. Сечение называется простым, если при удалении из него хотя бы одного ребра, оно перестает быть сечением. Утверждение: Для каждого ребра простого сечения найдется цепь, проходящая только через это ребро простого сечения. Если эта цепь идет в направлении этого ребра, то оно называется прямым, если против направления ребра, то обратным. Неориентированные ребра цепи всегда прямые. Пропускной способностью сечения W называется сумма W(c) пропускных способностей его прямых ребер. Теорема Форда-Фалкерсона Максимальная величина потока в сети равна минимальной пропускной способности его простых сечений.
УПРАЖНЕНИЯ 1. Перечислить все деревья, которые можно получить для 2, 3, 4, 5, 6 вершин. 2. Для графа, приведенного на рисунке построить все остовы. Рис.1 Рис.2 Рис.3
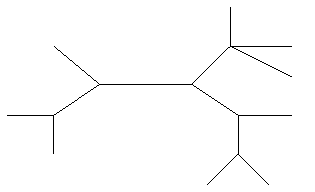
3. Для дерева приведенного на рисунке 7 определить вершины максимального типа, найти все диаметральные цепи. Убедится в том, что они проходят через центр.
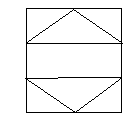
4. Для графов, приведенных на рисунке определить: цикломатическое число, число внутренней устойчивости и число внешней устойчивости.
Рис. 1 Рис. 2 Рис. 3 5. Источник информации может передавать код из 4-х различных однобуквенных сигналов
Определить, из каких сигналов надо составить код, чтобы исключить неправильное восприятие на приемной станции. Найти максимальное количество таких сигналов.
6. В пунктах
Можно ли расположить в каких либо из данных пунктов 4 или 3 источника, не поражающих друг друга?
7. Объекты
Рис. 3 Объекты, которые просматриваются друг из друга, соединены на рисунке ребром. Определить, в какие объекты достаточно поместить наблюдателей, чтобы они в совокупности просматривали все объекты.
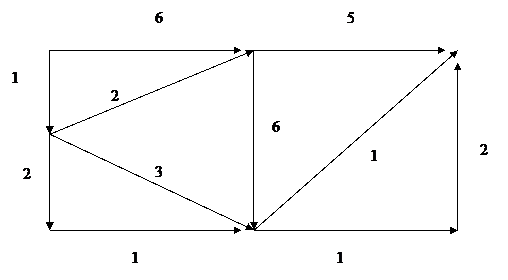
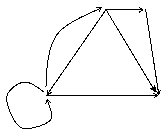
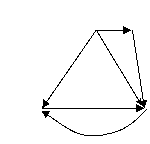
6. Для частично ориентированной сети привести два различных потока в сети, найти величину каждого потока. Перечислить все простые сечения сети. Определить максимальную величину потока, пользуясь теоремой Форда-Фалкерсона.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 431. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
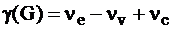 .
.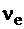 – число ребер графа G;
– число ребер графа G; 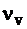 – число вершин;
– число вершин; 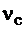 – число компонент связности.
– число компонент связности.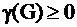 . Причем, если
. Причем, если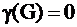 , то граф не имеет циклов, то есть является деревом или лесом;
, то граф не имеет циклов, то есть является деревом или лесом;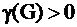 , то граф имеет ровно 1 цикл.
, то граф имеет ровно 1 цикл.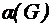 – это максимальное число несмежных вершин графа.
– это максимальное число несмежных вершин графа.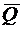 хотя бы одна дуга ведет в вершину множества Q. Если граф неориентированный, то число внешней устойчивости ищется для канонически соответствующего ориентированного графа.
хотя бы одна дуга ведет в вершину множества Q. Если граф неориентированный, то число внешней устойчивости ищется для канонически соответствующего ориентированного графа. – это мощность минимального внешне устойчивого множества.
– это мощность минимального внешне устойчивого множества.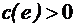 .
.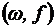 , где
, где 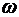 – некоторая ориентация неориентированных ребер сети, f = f(e), функция значения потока на ребре е, которая удовлетворяет следующим условиям:
– некоторая ориентация неориентированных ребер сети, f = f(e), функция значения потока на ребре е, которая удовлетворяет следующим условиям: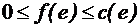
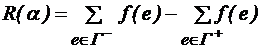 ,
,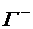 – множество ребер выходящих из вершины
– множество ребер выходящих из вершины 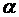 ,
,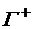 – множество ребер входящих в вершину
– множество ребер входящих в вершину 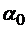 – входной полюс сети, а
– входной полюс сети, а 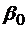 – выходной полюс, то
– выходной полюс, то .
.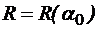 . Очевидно, что величина потока в сети зависит и от ориентации ребер
. Очевидно, что величина потока в сети зависит и от ориентации ребер 
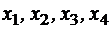 . Эти сигналы, в результате возникающего при передаче возмущения, воспринимаются на приемной станции как сигналы
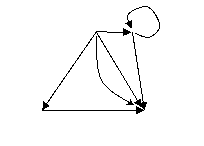
. Эти сигналы, в результате возникающего при передаче возмущения, воспринимаются на приемной станции как сигналы 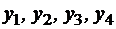 , причем могут иметь двойное истолкование, как, например, на рисунке 1.
, причем могут иметь двойное истолкование, как, например, на рисунке 1.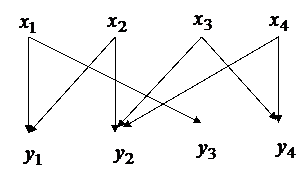
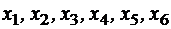 могут быть расположены источники излучения. Если источники расположенные в пунктах
могут быть расположены источники излучения. Если источники расположенные в пунктах 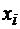 и
и 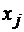 влияют друг на друга, то они соединены на рисунке ребром (см. рис. 2).
влияют друг на друга, то они соединены на рисунке ребром (см. рис. 2).
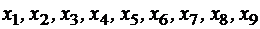 расположены так, как показано на рисунке 3.
расположены так, как показано на рисунке 3.