
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Записать условия перпендикулярности, параллельности прямой и плоскости.⇐ ПредыдущаяСтр 19 из 19 Пусть прямая задана каноническими уравнениями Прямая и плоскость параллельны тогда и только тогда, когда направляющий вектор прямой Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой Вычисление координат точки пересечения прямой и плоскости. Если точка принадлежит некоторой прямой, то координаты точки удовлетворяют уравнениям прямой. Аналогично, если точка лежит в некоторой плоскости, то координаты точки удовлетворяют уравнению этой плоскости. По определению точка пересечения прямой и плоскости является общей точкой прямой и плоскости, тогда координаты точки пересечения удовлетворяют как уравнениям прямой, так и уравнению плоскости. Пусть в прямоугольной системе координат Найдем координаты точки Искомые координаты точки пересечения прямой a и плоскости  Отметим, что при такой постановке задачи мы фактически находим координаты точки пересечения трех плоскостей, заданных уравнениями Если прямая а определена параметрическими уравнениями вида То если в уравнение Обратите внимание: если прямая Когда прямая a задана каноническими уравнениями вида 2.Функция: определение, способы задания, четность, периодичность, обратная функция. Графики функций:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 433. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , а плоскость общим уравнением
, а плоскость общим уравнением 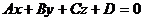 .
. и нормальный вектор плоскости
и нормальный вектор плоскости  перпендикулярны, то есть их скалярное произведение равно нулю
перпендикулярны, то есть их скалярное произведение равно нулю  – условие параллельности прямой и плоскости
– условие параллельности прямой и плоскости и нормальный вектор
и нормальный вектор  плоскости коллинеарны
плоскости коллинеарны  – условие перпендикулярности прямой и плоскости.
– условие перпендикулярности прямой и плоскости. заданы прямая a и плоскость
заданы прямая a и плоскость  , причем известно, что прямая a и плоскость
, причем известно, что прямая a и плоскость  .
. и
и  .
. . Это действительно так, так как решение системы линейных уравнений обращает каждое уравнение системы в тождество.
. Это действительно так, так как решение системы линейных уравнений обращает каждое уравнение системы в тождество.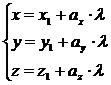 . ,
. , 
 , мы придем к уравнению с неизвестной
, мы придем к уравнению с неизвестной  . Разрешив это уравнение относительно
. Разрешив это уравнение относительно  , соответствующее координатам точки пересечения прямой a и плоскости
, соответствующее координатам точки пересечения прямой a и плоскости 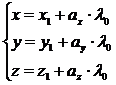 .
. ,
,  ,
,  , мы получим тождество
, мы получим тождество 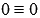 , а если указанная прямая параллельна плоскости - то мы получим неверное равенство.
, а если указанная прямая параллельна плоскости - то мы получим неверное равенство. . В этом случае для нахождения координат точки пересечения прямой a с плоскостью
. В этом случае для нахождения координат точки пересечения прямой a с плоскостью  ) и далее решать по аналогии.
) и далее решать по аналогии.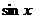 ,
,  ,
,  ,
,  . (2-ой вопрос как 2- ой вопрос билета 13 )
. (2-ой вопрос как 2- ой вопрос билета 13 )