
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Четность (нечетность функций),Функция у = f (х) называется четной, если для двух произвольных противоположных значений аргумента из области определения значения функции совпадают f (− х) = f (х), где График четной функции симметричен относительно оси Oy так как, по определению, вместе с любой своей точкой (х; у) он содержит и точку (- x, y). f (− х) = − f (х), где График нечетной функции симметричен относительно начала координат, так как, по определению, вместе с любой своей точкой (х; у) он содержит и точку (− х; − у). Периодичность (функций), · Функция у=f(х)называется периодической с периодом Т, если для каждого х из D(f) числа х+Т, x-T также принадлежат D(f) и при этом справедливо f(x+Т)=f(x)=f(x-T). · Наименьшее из положительных чисел Т называется основным периодом функции. Часто основной период функции называют просто ее периодом. Обратная функция. Если поменять ролями аргумент и функцию, то x станет функцией от y. В этом случае говорят о новой функции, называемой обратной функцией. Если функция g в каждой точке х области значений обратимой функции f принимает такое значение y, что f(y)=x, то говорят, что функция g — обратная функция к f. Или Определение:Пусть функция y=f(x) с областью определения D(f) и множеством значений R(f). Обратная к f — функция f−1 определяется как функция с областью определения D(f−1)=R(f) и множеством значений R(f−1)=D(f) , такая что f−1(y)=x тогда и только тогда, когда f(x)=y. Таким образом, f−1 возвращает y обратно в x.  Предположим, мы имеем функцию: v = u 2 , где Если обозначить аргумент в обеих функциях через x , а функцию – через y, то мы имеем две функции: Графики функций:
Билет 14 1. Записать векторное уравнение прямой в пространстве, Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки
Так как векторы Обозначив радиус-векторы точек получить канонический вид уравнений прямой в пространстве. Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz. Зададим в ней прямую. Выберем следующий способ задания прямой линии в пространстве: укажем точку, через которую проходит прямая a, и направляющий вектор прямой a. Будем считать, что точка Очевидно, что множество точек
Запишем необходимое и достаточное условие коллинеарности векторов разрешить относительно параметра Полученные уравнения вида Вывести параметрические уравнения прямой в пространстве, Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz. Зададим в ней прямую a, указав направляющий вектор прямой Пусть Очевидно, что множество точек
Запишем необходимое и достаточное условие коллинеарности векторов и представляет собой параметрические уравнения прямой a. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 675. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. - аргумент, a v - функция. Если поменять их ролями, то мы получим u как функцию v :
- аргумент, a v - функция. Если поменять их ролями, то мы получим u как функцию v : 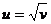 .
.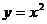 и
и  , каждая из которых является обратной по отношению к другой.
, каждая из которых является обратной по отношению к другой.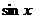 ,
,  ,
,  ,
,  .
.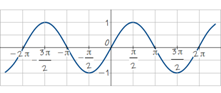 синус
синус


 и направляющего вектора
и направляющего вектора  , параллельного этой прямой.
, параллельного этой прямой. Пусть прямая проходит через точку
Пусть прямая проходит через точку  на прямой. Очевидно, что
на прямой. Очевидно, что  .
. и
и  коллинеарны, то найдется такое число
коллинеарны, то найдется такое число  , что
, что  , причем число
, причем число  на прямой. Множитель
на прямой. Множитель 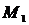 и
и  и
и  , получаем
, получаем  . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра
. Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра  лежит на прямой а и
лежит на прямой а и  - направляющий вектор прямой а.
- направляющий вектор прямой а.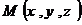 трехмерного пространства определяет прямую а тогда и только тогда, когда векторы
трехмерного пространства определяет прямую а тогда и только тогда, когда векторы  коллинеарны.
коллинеарны.
 . Теперь записываем условие коллинеарности векторов
. Теперь записываем условие коллинеарности векторов  и
и  :
: , где
, где  - произвольное действительное число (при
- произвольное действительное число (при  точки
точки  ,
,  ,
,  , то каждое уравнение системы
, то каждое уравнение системы 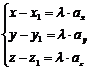 можно
можно
 в заданной прямоугольной системе координат Oxyz определяют прямую a. Уравнения
в заданной прямоугольной системе координат Oxyz определяют прямую a. Уравнения  , то есть,
, то есть, 
 , где
, где 