
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
А) аппроксимация полиномами.В методе наименьших квадратов аппроксимирующая функция y(x) ищется в виде суммы, аналогичной (5.3), но содержащей сравнительно небольшое число слагаемых:
Предполагая, что каким-то образом выбраны коэффициенты ak, тогда в каждой точке сетки (451) можно вычислить погрешность:
Функция δ, принимающая значения δ1, δ2, …, δn, представляет собой сеточную функцию и называется погрешностью решения . Сумма квадратов этих величин называется суммарной квадратичной погрешностью:
Возникает задача: найти такой набор коэффициентов ak, при которых суммарная квадратичная погрешность J оказывается минимальной. Функцию (5.9) с набором коэффициентов, удовлетворяющих этому требованию, называют наилучшим приближением по наименьших квадратов. Построение наилучшего приближения сводится к задаче поиска экстремума функции J от нескольких переменных:
Уравнения (4.12) можно переписать в виде:
где
Таким образом, получена система линейных алгебраических уравнений (5.14), в которой роль неизвестных играют искомые коэффициенты разложения a0, a1, … , am. Пример 5.2. Пусть известны экспериментальные значения концентрации некоторого вещества M в зависимости от времени протекания реакции:
Таблица 1.
Считая, что концентрация вещества описывается полиномом второй степени, определить его коэффициенты.
Решение: Здесь общее количество точек равно 5, степень полинома m=2, j0(х)=1, j1(х)=х, j2(х)=х2.  Для нахождения коэффициентов полинома, необходимо решить систему линейных уравнений. Определим ее коэффициенты:
g0,0=5, g0,1=250, g0,2=13¢500, g1,1=13¢500, g1,2=775¢000, g2,2=46¢590¢000 и коэффициенты, стоящие в правых частях системы: b0=5,895, b1=277,86, b2=14237,6 Итоговая система для определения коэффициентов имеет вид:
Для решения этой системы можно использовать любые имеющиеся пакеты математических прикладных программ, в том числе можно использовать и написанную программу для решения систем линейных алгебраических уравнений, приведенной в теме 2. Применяя эту программу, можно рассчитать коэффициенты а0, а1, а2. Окно ввода этой программы будет иметь вид:
Данные в программу вводятся согласно вышеописанной системе. После введения данных программа выдает исходную матрицу А и после этого преобразованную матрицу. Поскольку матрица верхнетреугольная, то при выводе второй и третьей строк они немного смещены влево относительно первой строки. В правой части каждой строки стоят значения bi. Значения полученных переменных даны в виде x[1], x[2], x[3]. Следует учитывать, что коэффициент x[1] – это коэффициент, стоящий при х2, т.е. а2 ; коэффициент х[2] это коэффициент, стоящий при х, т.е. а1; а x[3] – это коэффициент, стоящий без х, т.е. а0..
Зная эти значения, можно выписать уравнение квадратичной функции, аппроксимирующей экспериментальные данные: Р2(х) = 7×10-5 x2 - 0,024 x + 2,19 (5.15) Экспериментальные и расчетные значения показаны в таблице:
Рассчитаем суммарную квадратичную погрешность замены экспериментальных значений функцией вида (4.15):
Таким образом, найденная зависимость, описываемая уравнением (5.15), имеет достаточно хорошую согласованность с эмпирически полученными значениями М., что видно по следующему рисунку:
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 624. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (5.9)
(5.9) (5.10)
(5.10)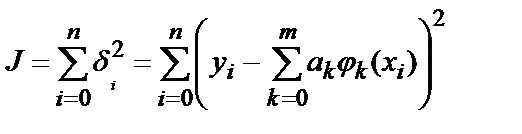 (5.11)
(5.11) (5.12)
(5.12) , l=0,1,…,m (5.13)
, l=0,1,…,m (5.13) (5.14)
(5.14) ,
, 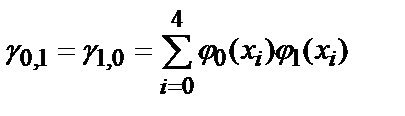 ,
, 
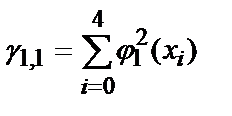 ,
,  ,
, 
 ,
,  ,
, 




