
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
По поиску собственных значений и векторов матрицMahCad позволяет определять значения собственных пар матриц с помощью встроенных функций: eigenvals и eigenvecs. Первая из них определяет весь набор собственных значений матрицы, включая комплексные, вторая – набор векторов (значения коэффициентов каждого вектора даются по столбцам) Пример 3.2. Дана матрица В, найти спектр матрицы:
Решение. Принимая за переменную Zn набор собственных значений матрицы В:
соответствующие им собственные вектора, переданные в переменную Ve, могут быть найдены посредством встроенной функции eigenvecs с аргументом B:
тогда матрица компонентов собственных векторов В будет иметь вид:
Если считать координаты собственных векторов вручную, то значения будут иные, это связано с тем, что MathCad переводит коэффициенты, стоящие при ξi , так чтобы длины получаемых собственных векторов были единичные. Приведем уравнения, связывающие компоненты вектора, при 𝝺1= 8,464 (это первый столбец Ve): 0,344 ξ1 =0,939 ξ2 или ξ1 =2,73 ξ2 Это же уравнение будет получено, если использовать коэффициенты какой-либо строки матрицы B – 𝝺1×E :
-1,464ξ1+ 4ξ2=0 Û 1,464 ξ1= 4ξ2 Û ξ1 =2,73 ξ2 Тогда вектор α1, соответствующий значению 𝝺1=8,464 имеет координаты (2,73а, а) или, согласно MathCad (0,939а;0,344а). Аналогичным образом могут быть получены коэффициенты второго вектора (-0,591а; 0,807а) или, например, (а;1,365а), матрица B – 𝝺2×E будет иметь вид:
Заметим, что при составлении уравнения вида (1), связывающего компоненты собственного вектора, коэффициенты из столбца берутся снизу вверх. Это правило работает для матриц любых размерностей. Пример 3.3. Так, в случае матрицы A (здесь она носит имя AN) из примера 2.1: 
Чтобы определить компоненты собственного вектора вручную, необходимо оставить два строки (любые) из матрицы AN – 𝝺1×E, например, первые две и приравнять их к нулю: (3-(-0,524))ξ1+ 2ξ2 + ξ3=0 ξ1+ (1-(-0,524))ξ2 - ξ3=0 после преобразований приходим к следующей системе (в качестве базисной переменной выбрана ξ1): ξ2 = -1,284ξ1 ξ3 = -0,957ξ1 Следовательно, первый собственный вектор (при 𝝺1 = -0,524) будет иметь компоненты (а; -1,284а; -0,957а) или, согласно MathCad Отметим, что для того, чтобы получить коэффициенты, аналогичные последнему приведенному вектору, необходимо отнормировать коэффициента вектора, полученного вручную, то есть добиться его единичной длины.
Задание для лабораторной работы №3: Задание 1. Найти все собственные значения и вектора матрицы А вручную: 6+N 4 A= 8 15-N Задание 2. Найти все собственные значения и вектора матрицы А
Посредством использования стандартных функций пакета MathCad. Контрольные вопросы 1. Какой вектор называется собственным вектором матрицы? 2. Какое число называется собственным значением матрицы? 3. Что такое собственная пара матрицы? 4. Какое уравнение называется вековым? 5. Что такое спектр матрицы? ТЕМА 4. МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ Пусть рассматривается некий процесс, зависящий от одного параметра х и описываемый функцией y=f(x). Поставим задачу: определить такие значения параметра х, равные х*, которые вызывают остановку процесса, то есть выполнение условия: f(x)=0 (4.1) Теорема о существовании нуля непрерывной функции: Если функция f(x) непрерывна на отрезке [a,b] и принимает на его концах значения разных знаков, то на этом отрезке существует по крайней мере один корень уравнения (3.1). Пусть известно, что на [a,b] существует единственный корень уравнения (1). Потребуем, чтобы функция: 1) была непрерывна на [a,b] вместе со своими производными f¢(x) и f²(x); 2) в точках a и b функция имеет разные знаки, т.е. f(a)×f(b)<0; 3) производные f¢(x), f²(x) – сохраняют знак на всем [a,b], т.е. функция должна быть строго монотонной на [a,b].
an £ х* £ bn. (4.2) Это двойное неравенство показывает, что число an определяет х* с недостатком, а число bn – с избытком. За решение уравнения (4.1) принимается значение x*=(an + bn)/2 при условии, что Dn < e (4.3) где Dn = |bn – an|, а e - заданная точность. Очевидно, что скорость сходимости метода половинного деления будет равна ½. Метод итераций.Предположим, что уравнение (3.1) можно переписать в виде: x=j(x) (4.4) Возьмем произвольное значение х0 из области определения функции j(x) и будем строить последовательность чисел {xn}, определенных с помощью рекуррентной формулы xn+1 = j(xn), n=0, 1, 2, … (4.5) Последовательность {xn} называется итерационной последовательностью. Точность найденного решения определяется формулой (4.3): Dn = |xn – xn-1| < e (4.6) где e - заданная точность. Метод хорд. Будем полагать, что функция f(x) дважды дифференцируема на [a,b] функция.
Метод хорд требует, чтобы один конец отрезка [a,b], был неподвижен. Условие неподвижности точки: f ”(xн) × f(xн) > 0 (4.7) Расчетная формула для определения n-ого приближения:
При выполнении условия (4.6) за решение принимается х*=xn. Метод касательных (метод Ньютона). Будем полагать, что функция f(x) – это дважды дифференцируемая на [a,b] функция. Метод заключается в следующем: из точки, для которой выполняется условие (4.7) испускается касательная к кривой y=f(x), которая пересекает ее в точке х1 – эта точка станет первым приближением к корню х*, затем вновь проводим касательную к кривой в точке (х1,f(x1)) – получим х2 и т.д.
Комбинированный метод хорд и касательных.Для ускорения сходимости используют комбинированный метод хорд и касательных. Здесь одновременно из точки (b,f(b)) проводят касательную, а из точки (a,f(a)) – хорду. Получается новый интервал (a1, b1) и процедура повторяется до выполнения условия
В это)м случае за «истинное» решение уравнения (4.1) можно принять значение
Пример 4.1. Найти решение уравнения f(x)=x-cos(x)=0 на отрезке [0,1] с ε=0, 01 с помощью каждого описанного метода. Решение: Для этой функции на указанном отрезке выполняются следующие условия: f’>0, f’’>0. Следующая таблица показывает работу метода половинного деления:
Как видно из таблицы на 7 -ой итерации получен корень уравнения х=0,738. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой) Замечание. Для метода половинного деления всегда можно определить количество требуемых итераций по формуле: n > log2 ((b-a)/e) где n – ближайшее большее целое число. Следовательно, для нашей задачи: n > log2 ((1-0)/0.01) = log2100 = 6.64 , то есть n=7, что и видно из таблицы. Последовательность вложенных сегментов имеет вид: -[0,1]+ É -[0.5,1]+ É -[0.5,0.75]+ É -[0.625,0.75]+ É -[0.688,0.75]+ É -[0.719,0.75]+ É -[0.734,0.75]+ É -[0.734,0.742]+ É 0.738 Верхние индексы, стоящие слева и справа от отрезка, показывают знак функции соответственно в левом и правом конце интервала. Метод итераций.
Как видно из таблицы на 11 -ой итерации получен корень уравнения х=0,742. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой) Замечание. Для нулевой итерации за х0 взяли среднее значение между a и b, равное 0,5. Метод хорд. Определим неподвижную точку, для этого проверим условие (4.7) в точках a и b: f ”(а) × f(а) < 0, f”(b) × f(b) > 0 Значит, неподвижной точкой является точка b. Таблица по работе метода хорд имеет вид:
Как видно из таблицы на 3 -ей итерации получен корень уравнения x=0,739. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой) Последовательность вложенных сегментов имеет вид: -[0,1]+ É -[0.685,1]+ É -[0.736,1]+ É -[0.739,1]+ É 0.739 Верхние индексы, стоящие слева и справа от отрезка, показывают знак функции соответственно в левом и правом конце интервала. Метод касательных.
Как видно из таблицы на 3 -ей итерации получен корень уравнения x=0,739. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой) Последовательность вложенных сегментов имеет вид: -[0,1]+ É -[0,755]+ É -[0,0.739]+ É -[0,0.739]+ É 0.739. Верхние индекс, стоящие слева и справа от отрезка, показывают знак функции соответственно в левом и правом конце интервала. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 599. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||









 (4.8)
(4.8) (4.9)
Точка xnбудет являться корнем уравнения (4.1) при выполнении (4.6).
Геометрическое представление метода показано на рисунке:
(4.9)
Точка xnбудет являться корнем уравнения (4.1) при выполнении (4.6).
Геометрическое представление метода показано на рисунке:
 (4.10)
(4.10)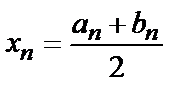 (4. 11)
(4. 11)