
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методы определения потребности в основных материалах- метод прямого счета где Рм – потребность в основных материалах; Нi – норма расхода материала на i-ое изделие; Vi – производство i-го изделия. - метод аналогии (при производстве нового изделия) где Нб – норма расхода материала на аналогичное базовое изделие; Vн – плановый выпуск нового изделия; К- коэффициент, учитывающий особенности потребления материала при производстве нового изделия (отношение массы нового и базового изделий). - метод динамических коэффициентов (отсутствуют данные о производственной программе, норме расхода МР). где Рф – фактический расход материалов за прошедший период; I1 – индекс изменения производственной программы; I2 – индекс изменения норм расхода материалов в плановом периоде. - метод скользящей средней исходит из предложения, что прогнозируемая величина равна средней за последние три месяца. - метод экспоненциального сглаживания применяется в тех случаях, когда нет тренда (основных тенденций развития потребности). Прогнозируемая величина рассчитывается по формуле (5).
уt+1= a× уt + a× (1- a)× уt-1 + a× (1- a )2× уt-2 + a× (1- a)R t-R + ... + у0(1-a )t-1 , (5)
где уt+1 - прогнозируемая величина; a - коэффициент сглаживания; у0 - начальное значение. a=  где n - число уровней ряда. - метод корреляционно-регрессионного анализа.В рамках метода устанавливается взаимосвязь между рассматриваемыми показателями и теснота этой связи. Корреляционный анализ может использовать взаимосвязь между 2-мя показателями (парная корреляция) или несколькими (множественная корреляция). Уравнение линейной регрессии y=a+bx,где х- объёмы , у - потребность Коэффициенты a и b находят статистическим путем по формуле (7). Для того чтобы определить тесноту связи между рассматриваемыми показателями необходимо рассчитать коэффициент корреляции. Если коэффициент приближается к 1, то наблюдается линейная зависимость. Если ближе к 0, то связь между параметрами отсутствует связь, если стремиться -1, то связь обратная. Коэффициент корреляции определяют по формуле (8).
- метод экстраполяции трендовиспользуют в тех случаях, когда наблюдаются тенденции в поведении изучаемого показателя, например: потребности в ресурсах, объема закупок (поставок). Для того чтобы установить, существует ли тренд, необходимо графически отобразить поведение показателя и рассчитать коэффициент корреляции. Если çrç ñ 0,7, то тренд имеет ярко выраженную устойчивую зависимость; çrçá 0,3, то тренд отсутствует; 0,3£½r½³0,7, тренд имеет неустойчивую тенденцию. При криволинейной зависимости коэффициент корреляции примерно оценивает тесноту связи, в этом случае в качестве меры тесноты связи используют корреляционное отношение. Численное равенство между r и h свидетельствует о линейной зависимости между признаками. При выборе трендовых моделей необходимо учитывать основные тенденции показателя. Параметры модели рассчитываются при помощи метода наименьших квадратов. Расчет можно провести и по упрощенным формулам с введением условного уровня ряда.
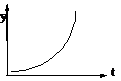
Трендовые криволинейные модели
Точность прогноза определяется по формуле (9)
где S - ошибка прогноза; n- число уровней ряда; k- число параметров в уравнении. Использование метода на основе рядов динамики, метода экстраполяции трендов позволяет изучить основную тенденцию развития показателя (тренд). В конкретном случае изучаемым показателем являются объемы выпуска продукции. В основе метода экстраполяции трендов лежит построение адекватной математической функции (трендовой модели), которая наилучшим образом отображает основную тенденцию развития спроса. В табл. 3.4 содержится информация о правильности выбора адекватной математической функции (трендовой модели). Расчет параметров “а” и “b” осуществляется при помощи метода наименьших квадратов. Криволинейные функции необходимо линеаризовать, то есть привести к линейному виду посредством обратных преобразований и натуральных логарифмов. В некоторых случаях спрос и потребление носят сезонный характер. Сезонные колебания происходят внутри общего тренда и ограничиваются изменениями в течение одного года. Для определения сезонной структуры необходимо собрать информацию о нескольких временных периодах в пределах года, обычно это месячные или квартальные данные. После соответствующей обработки статистических данных и установления временных периодов находят суммарное значение спроса. Затем полученная сумма делится на число лет - n. Полученные средние значения для каждого периода являются в то же время и оценкой для следующего периода при отсутствии серьезных изменений в тренде. Показатели сезонных колебаний остаются относительно постоянными. Для эффективного управления закупками требуется точное определение потребности в материальных ресурсах, независимо от выбранного метода, так как ошибка (погрешность), содержащаяся в прогнозе, может привести к неправильным решениям и дать отрицательный экономический эффект. Наилучшей аппроксимацией прогнозирующей функции является аппроксимация, минимизирующая стандартное отклонение как погрешность в оценке. Если нет уверенности в том, что тот или иной вид прогнозирующей функции заведомо предпочтительнее других, то следует испытать несколько различных форм прогнозирующей функции и выбрать наилучшую в соответствии с критерием минимизации стандартного отклонения. Часто количественные методы прогнозирования сочетаются с качественными (методами экспертных оценок). Необходимость использования эвристического подхода обусловлена отсутствием некоторой информации, получение которой невозможно или связано с большими затратами времени и средств. Разработка прогнозов потребности в материальных ресурсах оказывает большую помощь при планировании материально-технического обеспечения. Все рассмотренные методы имеют достоинства и недостатки с точки зрения точности определения потребности в ресурсах, затрат времени и стоимости услуг. Выбор зависит от размеров предприятия, наличия и видов складов, системы контроля над уровнем запасов. Важно отметить: процесс планирования потребности в материальных ресурсах должен осуществляться параллельно с согласованием противоречивых интересов во всех подсистемах (снабжение, производство, сбыт) с целью разработки наиболее оптимальной программы производства.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 364. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (1)
, (1)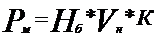 , (2)
, (2)  , (4)
, (4)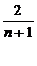 , (6)
, (6) , (7)
, (7)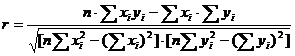 , (8)
, (8) ;
;  ;
;


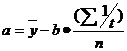 ;
; 
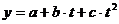
 ;
; 
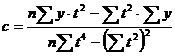 Формулы расчета упрощенные
Формулы расчета упрощенные

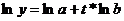
 ;
; 


 ;
; 


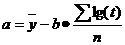 ;
; 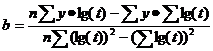
 , (9)
, (9)