Лемма Арцелы (критерий компактности).
def: Семейство  , функций , функций  называется равномерно ограниченными, если называется равномерно ограниченными, если  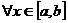   . Здесь и в дальнейшем . Здесь и в дальнейшем  . .
def: Семейство  , функций , функций  называется равномерно непрерывными, если называется равномерно непрерывными, если 
Пример 1:
Пусть даны числа  и и  положим положим  - множество тех функций - множество тех функций  (условие Гёльдера порядка (условие Гёльдера порядка 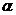 ), тогда ), тогда  равностепенное, непрерывное семейство. Фиксируем равностепенное, непрерывное семейство. Фиксируем  , , 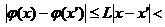  из этого следует, что можно взять любое из этого следует, что можно взять любое  . Однако, . Однако,  не является равномерно ограниченной, так как не является равномерно ограниченной, так как  содержит все константы. содержит все константы.
Пример 2:
Возьмем  тогда тогда  − равномерно ограничено − равномерно ограничено  . Покажем, что семейство . Покажем, что семейство  не является равностепенно непрерывным, то есть выполнено его отрицание не является равностепенно непрерывным, то есть выполнено его отрицание  . Положим . Положим  . Пусть . Пусть  - произвольное малое число. Выберем - произвольное малое число. Выберем  , тогда , тогда 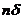 больше периода функции больше периода функции  , из этого следует, что на любом интервале длины , из этого следует, что на любом интервале длины  существуют точки существуют точки  и и  для которых для которых  , а , а  . В этом случае . В этом случае  , следовательно , следовательно  не является равностепенно непрерывным. не является равностепенно непрерывным.
Лемма Арцелы (Arzela – итал.)
Пусть  - равномерно ограниченное и равномерно непрерывное семейство функций - равномерно ограниченное и равномерно непрерывное семейство функций  , тогда из каждой последовательности , тогда из каждой последовательности 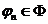 можно выделить последовательность можно выделить последовательность  равномерно сходящейся к непрерывной функции равномерно сходящейся к непрерывной функции  ( (  может не принадлежать семейству может не принадлежать семейству  ). ).
Пример:
 тогда тогда  , но , но 
Доказательство
◄ Пусть  ,… – все рациональные точки на ,… – все рациональные точки на 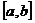 . Поскольку . Поскольку  - ограниченное множество в - ограниченное множество в  (в силу равномерной ограниченности (в силу равномерной ограниченности  ), то существует подпоследовательность ), то существует подпоследовательность  последовательности последовательности  такая, что такая, что  фундаментальна в фундаментальна в  (по теореме Больцано – Вейерштрассе). Поскольку (по теореме Больцано – Вейерштрассе). Поскольку  ограничена в ограничена в  то существует подпоследовательность то существует подпоследовательность  последовательности последовательности  такая, что такая, что  фундаментальна в фундаментальна в  . Поскольку . Поскольку  ограничена в ограничена в  то существует подпоследовательность то существует подпоследовательность  последовательности последовательности  такая, что такая, что  фундаментальна в фундаментальна в  и так далее. Получим семейство последовательностей: и так далее. Получим семейство последовательностей:

Выберем диагональную подпоследовательность  (метод Кантора). Покажем, что (метод Кантора). Покажем, что  искомая подпоследовательность. Докажем, что искомая подпоследовательность. Докажем, что  равномерно фундаментальна на равномерно фундаментальна на 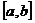 , то есть , то есть  . В силу равностепенной непрерывности семейства . В силу равностепенной непрерывности семейства   . Разобьем . Разобьем 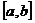 на равные отрезки длины меньше на равные отрезки длины меньше  . Тогда . Тогда  : в каждом отрезке этого разбиения есть хотя бы одна точка из : в каждом отрезке этого разбиения есть хотя бы одна точка из 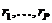 (пусть отрезок разбит на M частей; для каждой части выбирают (пусть отрезок разбит на M частей; для каждой части выбирают  и выбираем и выбираем  ). В силу плотности рациональных чисел на ). В силу плотности рациональных чисел на 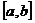 . Заметим что . Заметим что  – фундаментальна в – фундаментальна в   так как так как  - подпоследовательность последовательности - подпоследовательность последовательности  , начиная с , начиная с 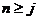 . .

Далее,  , ,  . .
Покажем, что это N – искомое   . .
Пусть  , ,  , тогда х принадлежитнекоторому отрезку разбиения. В этом отрезке есть хотя бы одна из точек , тогда х принадлежитнекоторому отрезку разбиения. В этом отрезке есть хотя бы одна из точек 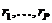 , например , например 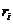 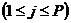 ( (  и и 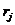 могут быть на концах отрезка разбиения). Заметим могут быть на концах отрезка разбиения). Заметим  . .
Имеем
 ( (  ). ).
Итак,  равномерно фундаментальна на равномерно фундаментальна на 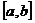 . Поэтому при каждом фиксированном . Поэтому при каждом фиксированном  последовательность последовательность  - фундаментальна в - фундаментальна в  и следовательно по критерию Коши сходится в и следовательно по критерию Коши сходится в  к некоторому элементу к некоторому элементу  . Устремим в ( . Устремим в ( 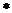 ) m к ) m к  . Получим, что . Получим, что   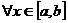 : :  . Это означает, что . Это означает, что  сходится равномерно к сходится равномерно к  на на 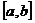 . Поскольку . Поскольку  – непрерывна на – непрерывна на 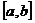 , то по теореме из анализа , то по теореме из анализа  так же непрерывна на так же непрерывна на 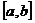 . Лемма доказана ► . Лемма доказана ►
|


 , функций
, функций  называется равномерно ограниченными, если
называется равномерно ограниченными, если 
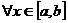

 . Здесь и в дальнейшем
. Здесь и в дальнейшем  .
.
 и
и  положим
положим  (условие Гёльдера порядка
(условие Гёльдера порядка 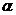 ), тогда
), тогда  ,
, 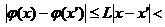
 из этого следует, что можно взять любое
из этого следует, что можно взять любое  . Однако,
. Однако,  тогда
тогда  . Покажем, что семейство
. Покажем, что семейство  . Положим
. Положим  . Пусть
. Пусть  - произвольное малое число. Выберем
- произвольное малое число. Выберем  , тогда
, тогда 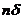 больше периода функции
больше периода функции  , из этого следует, что на любом интервале длины
, из этого следует, что на любом интервале длины  существуют точки
существуют точки  и
и  для которых
для которых  , а
, а  . В этом случае
. В этом случае  , следовательно
, следовательно 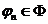 можно выделить последовательность
можно выделить последовательность  равномерно сходящейся к непрерывной функции
равномерно сходящейся к непрерывной функции  может не принадлежать семейству
может не принадлежать семейству  тогда
тогда  , но
, но 
 ,… – все рациональные точки на
,… – все рациональные точки на 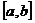 . Поскольку
. Поскольку  - ограниченное множество в
- ограниченное множество в  (в силу равномерной ограниченности
(в силу равномерной ограниченности  последовательности
последовательности  такая, что
такая, что  фундаментальна в
фундаментальна в  ограничена в
ограничена в  последовательности
последовательности  фундаментальна в
фундаментальна в  ограничена в
ограничена в  последовательности
последовательности  фундаментальна в
фундаментальна в 
 (метод Кантора). Покажем, что
(метод Кантора). Покажем, что  . В силу равностепенной непрерывности семейства
. В силу равностепенной непрерывности семейства  . Разобьем
. Разобьем  : в каждом отрезке этого разбиения есть хотя бы одна точка из
: в каждом отрезке этого разбиения есть хотя бы одна точка из 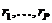 (пусть отрезок разбит на M частей; для каждой части выбирают
(пусть отрезок разбит на M частей; для каждой части выбирают  и выбираем
и выбираем  ). В силу плотности рациональных чисел на
). В силу плотности рациональных чисел на  – фундаментальна в
– фундаментальна в  так как
так как  , начиная с
, начиная с 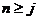 .
.
 ,
,  .
.
 .
. ,
,  , тогда х принадлежитнекоторому отрезку разбиения. В этом отрезке есть хотя бы одна из точек
, тогда х принадлежитнекоторому отрезку разбиения. В этом отрезке есть хотя бы одна из точек 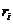
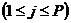 (
( 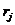 могут быть на концах отрезка разбиения). Заметим
могут быть на концах отрезка разбиения). Заметим  .
. (
( 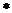 ).
). - фундаментальна в
- фундаментальна в  . Устремим в (
. Устремим в (  . Получим, что
. Получим, что 

 . Это означает, что
. Это означает, что  на
на