
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Канонические и нормальные системы ОДУ. Порядок системы. Сведение системы к одному уравнению и наоборот.Стр 1 из 16Следующая ⇒ Обыкновенные Дифференциальные Уравнения (ОДУ). Лекции Семестр. Лектор: Сухинин М. Ф. Оглавление Канонические и нормальные системы ОДУ. Порядок системы. Сведение системы к одному уравнению и наоборот....................................................................................................................................... 3 Лемма Арцелы (критерий компактности)................................................................................ 5 Ломаные Эйлера и теорема Пеано............................................................................................ 7 Теорема о единственности решения задачи Коши для систем ОДУ. Следствие для ОДУ n-го порядка. Случай линейного уравнения и линейной системы............................................................... 8 Лемма о равномерной непрерывности................................................................................... 11 Непрерывность решения системы ОДУ по начальным данным и параметру................... 11 Линейная зависимость и независимость вектор-функций. Определитель Вронского..... 13 Фундаментальная система решений (ФСР) для линейной однородной системы ОДУ. Существование ФСР и их взаимосвязь. Общее решение линейной однородной неоднородной системы............ 15 Резольвента линейной системы ОДУ и ее свойства............................................................. 16 Построение линейной, однородной системы по известной ФСР. Формула Лиувилля... 17 Нахождение частного решения линейной неоднородной системы ОДУ методом вариации постоянных. Формула Коши.......................................................................................................................... 18 Линейные системы с постоянными коэффициентами и методы их решения Случай нормализуемой системы...................................................................................................................................... 18 Линейные системы с постоянными коэффициентами и методы их решения Случай не нормализуемой системы...................................................................................................................................... 20  Нормальные линейные системы с постоянными коэффициентами и методы их решения 21 Устойчивость решения по Ляпунову и асимптотическая устойчивость. Лемма Ляпунова об устойчивости...................................................................................................................................................... 24 Лемма Ляпунова об асимптотической устойчивости и ее усиленный вариант................ 25 Теорема Ляпунова об асимптотической устойчивости по линейному приближению..... 28 Лемма Адамара.......................................................................................................................... 30 Дифференцируемости решения системы ОДУ по начальным данным и параметру........ 30 Первые интегралы систем дифференциальных уравнений. Задание общего решения системы с помощью полной системы первых интегралов...................................................................................... 33 Существование полной системы первых интегралов.......................................................... 34 Линейные однородные УрЧП первого порядка. Связь с первыми интегралами соответствующей системы ОДУ. Замечание о квазилинейных уравнениях.................................................................... 35 Квазилинейные УрЧП первого порядка. Две леммы о характеристиках........................... 38 Теорема о существовании единственного решения задачи Коши для квазилинейных УрЧП первого порядка в случае пространственных переменных............................................................................... 40 Оператор Штурма-Лиувилля. Его собственные функции. Лемма о нулевом собственном значении. 43 Представление решения краевой задачи для уравнения Штурма-Лиувилля через функцию Грина. Выражение функции Грина и ее свойства............................................................................. 44 Канонические и нормальные системы ОДУ. Порядок системы. Сведение системы к одному уравнению и наоборот.
Системой ОДУ называется система вида:
где
Система (2) называется канонической, число Вектор – функция
где Введем новые неизвестные функции:
Тогда (2) сводится к виду: (5)
Системы (2) и (5) эквивалентны, система (5) нормальная. Порядки систем (2) и (5) одинаковы и равны
Продифференцируем первое уравнение из (3) один раз, два раза, …
Допустим, что
Подставим эти соотношения в последнее уравнение из (6), получим Пример:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 636. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
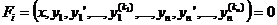 (1)
(1) . Пусть
. Пусть  и якобиан
и якобиан  , тогда по теореме о неявной функции можно выразить
, тогда по теореме о неявной функции можно выразить  через остальные переменные то есть
через остальные переменные то есть (2).
(2).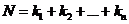 называется порядком системы (2). Вектор – функция
называется порядком системы (2). Вектор – функция  называется решением системы (1) или (2), если при подстановке этой вектор – функции в систему (1) или (2) получаем тождество.
называется решением системы (1) или (2), если при подстановке этой вектор – функции в систему (1) или (2) получаем тождество. называется общим решением уравнений (1) или (2) в области
называется общим решением уравнений (1) или (2) в области 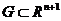 или
или  , если каждое решение системы (1) или (2), график которого лежит в G, может быть представлена в виде:
, если каждое решение системы (1) или (2), график которого лежит в G, может быть представлена в виде:  при некотором наборе констант
при некотором наборе констант  Система вида:
Система вида: (3)
(3) ,
,  называется нормальной. Произвольная каноническая система (2) может быть сведена к нормальной с помощью введения новых неизвестных функций.
называется нормальной. Произвольная каноническая система (2) может быть сведена к нормальной с помощью введения новых неизвестных функций. (4)
(4)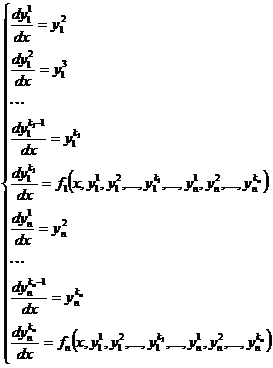
 (3)
(3) раз (если это возможно):
раз (если это возможно): (6).
(6). в рассматриваемой области, тогда по теореме о неявной функции можно выразить
в рассматриваемой области, тогда по теореме о неявной функции можно выразить  через остальные переменные, то есть
через остальные переменные, то есть .
. - ОДУ n-го порядка. Такое сведение не всегда возможно.
- ОДУ n-го порядка. Такое сведение не всегда возможно. , здесь
, здесь 