
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Понятие функции действительной переменной,способы задания и простейшие классы функций3. Суперпозиция функций, обратная, неявная и параметрическая функции 4. Классификация элементарных функций Введение Этой лекцией начинается одна из важных тем «Математический анализ», посвященных в основном исследованию функций. В предыдущем семестре в теме «Теория множеств» было изучено понятие функции на множестве. Очередные несколько лекций будут посвящены этим функциям, но только для действительных множеств. Напомним, что функцией называется любое бинарное отношение, которое не содержит двух пар с одинаковыми первыми элементами и разными вторыми, или другими словами, единственному элементу одного множества некоторым образом соответствует единственный элемент другого множества. При изучении лекции следует обратить внимание и сравнить уже известные понятия «суперпозиция» и «обратная функция» из теории множеств (см. л. 1 – 4, ч. 1) с аналитическим способом задания функции в данной лекции. Рассмотрим множество действительныхчисел R, на котором будут задаваться функции, а также его свойства. Множество действительных чисел и его свойства
Определение 1. Дельта-окрестностью точки Возьмем некоторое множество
1. Упорядоченность.
2. Плотность. 
3. Непрерывность.
Понятие функции действительной переменной, Способы задания и простейшие классы функций Понятие функции действительной переменной Зададим два множества Определение 2. Отображение D из множества R на E из множества R, которое ставит в соответствие элементу множества D единственный элемент множества E, называется функцией. Обозначается Способы задания функции
2. Графический способ. В виде графической зависимости (рис. 3) переменной y от независимого аргумента x. Преимущества такого способа – наглядность, возможность найти значение функции для любого аргумента. Недостатком – низкая точность, невозможность анализа функции. 3. Табличный способ.
 В виде табличной (известной еще со школьного курса) зависимости переменной y от независимого аргумента x (рис.4). Преимущество такого способа – быстрота определения значений функции в зависимости от аргумента. Недостатками являются низкая точность, невозможность анализа функции, ненаглядность, невозможность определения значения функции для любого значения аргумента. В виде табличной (известной еще со школьного курса) зависимости переменной y от независимого аргумента x (рис.4). Преимущество такого способа – быстрота определения значений функции в зависимости от аргумента. Недостатками являются низкая точность, невозможность анализа функции, ненаглядность, невозможность определения значения функции для любого значения аргумента.
2.3. Простейшие классы функций Определение 3. Функция Определение 4. Функция Определение 5. Функция Можно показать, что функция, удовлетворяющая равенству (1), удовлетворяет и равенству За период принимают наименьшее значение l, от прибавления которого значение функции не изменяется. Определение 6. Функция Определение 7. Функция
В определении функции подчеркивалось, что ПРИМЕР 1.
3. Суперпозиция функций, обратная, неявная и параметрическая функции 3.1. Суперпозиция функций Пусть Определение 8. Отображение ПРИМЕР 2. 3.2. Обратная функция Если между множествами Замечание! Графики взаимно обратных функций симметричны относительно оси 3.3. Параметрическая функция Определение 9. Задание функции, при котором обе переменные, связанные функционально, выражаются через переменную t – параметр, называется параметрическим.
3.4. Неявная функция Определение 10. Задание функции равенством, неразрешенным относительно самой функции, называется неявным.
ПРИМЕР 4.
4. Классификация элементарных функций Основные элементарные функции: 1. Степенная функция 2. Показательная функция 3. Логарифмическая функция 4. Тригонометрические функции 5. Обратные тригонометрические функции
Элементарными функциями называются функции, полученные с помощью конечного числа арифметических операций и суперпозиций функций. Все элементарные функции делятся на два класса – алгебраические и трансцендентные. Определение 12. Алгебраические – это функции, полученные из независимой переменной посредством операций В свою очередь алгебраические функции делятся на рациональные, т. е. не содержащие операций возведения в дробную степень, и на иррациональные, содержащие такую операцию. В свою очередь рациональные функции делятся на целые и дробные.
Целой рациональной функцией или многочленом называется функция вида Определение 14. Дробной рациональной функцией называется отношение целых функций Замечание! Все неалгебраические функции называются трансцендентными ( Заключение На этой лекции рассмотрены основные способы задания функций и их классификация, поэтому ее понимание очень важно на протяжении изучения всего курса высшей математики. Рекомендуется для лучшего усвоения следующих разделов высшей математики возвращаться к данной лекции. Отметим что: - множество действительных чисел упорядоченное, плотное и непрерывное; - дельта-окрестность может быть бесконечно малой; - понятие сложной функции основано на понятии суперпозиции отношений; - понятие обратной функции основано на понятии обратного отношения; - не явная функция не разрешена относительно переменной; - параметрическое задание функции определяется через третий параметр; - функции бывают четные, нечетные и периодические; - все функции бывают алгебраические ( Литература 1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001. 2. Натансон И.П. Теория функций вещественной переменной. – СПб.: Лань, 1999. - 560 с. 3. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с.
Цель лекции: изучить понятие предела, научиться доказывать теоремы с применением понятий предела, понять геометрический смысл дельта-окрестности. План лекции |
||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 651. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Итак, предметом математического анализа является функция и ее свойства. Основной метод математического анализа – предельный переход.
Итак, предметом математического анализа является функция и ее свойства. Основной метод математического анализа – предельный переход. называется множество точек, таких, что расстояние от любой точки x этого множества до точки
называется множество точек, таких, что расстояние от любой точки x этого множества до точки  меньше дельта, или
меньше дельта, или  .
. ~R, тогда графически дельта-окрестность может быть представлена на рис. 1.
~R, тогда графически дельта-окрестность может быть представлена на рис. 1.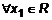 и
и  справедливо только одно из унарных отношений:
справедливо только одно из унарных отношений:  ,
,  ,
,  .
. при
при  .
. и
и 
 :
:  .
. и
и  , обозначив их элементы
, обозначив их элементы  и
и  соответственно.
соответственно. или
или  , или
, или  . При этом x – независимый аргумент, y – зависимая переменная (функция). D – область определения функции, E – множество ее значений.
. При этом x – независимый аргумент, y – зависимая переменная (функция). D – область определения функции, E – множество ее значений. 1. Аналитический способ.
1. Аналитический способ. В виде аналитического выражения (рис. 2) зависимой переменной y от независимого аргумента x. Преимущества такого способа – компактность записи, возможность найти значение функции для любого аргумента и точность. Недостатками являются отсутствие наглядности, громоздкость вычислений.
В виде аналитического выражения (рис. 2) зависимой переменной y от независимого аргумента x. Преимущества такого способа – компактность записи, возможность найти значение функции для любого аргумента и точность. Недостатками являются отсутствие наглядности, громоздкость вычислений. называется четной, если справедливо
называется четной, если справедливо 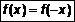 , то есть если точка (x,y) принадлежит графику четной функции, то и точка (-x,y) также принадлежит этому графику. График функции симметричен относительно оси Oy.
, то есть если точка (x,y) принадлежит графику четной функции, то и точка (-x,y) также принадлежит этому графику. График функции симметричен относительно оси Oy. , то есть если точка (x,y) принадлежит графику четной функции, то и точка (-x,-y) также принадлежит этому графику. График функции симметричен относительно начала координат.
, то есть если точка (x,y) принадлежит графику четной функции, то и точка (-x,-y) также принадлежит этому графику. График функции симметричен относительно начала координат. . (1)
. (1) , где
, где  . То есть
. То есть  .
.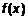 - монотонно возрастающая на множестве M, если
- монотонно возрастающая на множестве M, если  и
и  из неравенства
из неравенства  следует
следует  .
. и
и  из неравенства
из неравенства  .
.
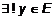 . Определенная таким образом функция называется однозначной. Иногда приходится расширить понятие функции до неоднозначного:
. Определенная таким образом функция называется однозначной. Иногда приходится расширить понятие функции до неоднозначного:  .
.
 ,
, 
 . В этом случае функция многозначна.
. В этом случае функция многозначна. и
и  ,
,  ,
,  .
.  :
:  , которое каждому элементу x из X ставит в соответствие элемент z из Z, называется сложной функцией или суперпозицией функции (см. л. 4, ч. 1) или функцией от функции.
, которое каждому элементу x из X ставит в соответствие элемент z из Z, называется сложной функцией или суперпозицией функции (см. л. 4, ч. 1) или функцией от функции.  . (2)
. (2) .
. на
на  , или о функции
, или о функции  , или
, или  , или
, или  . Полученная таким образом функция называется обратной функцией (см. лекция 4, часть 1).
. Полученная таким образом функция называется обратной функцией (см. лекция 4, часть 1). .
. . (3)
. (3)

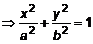 – эллипс.
– эллипс. . (4)
. (4) , следовательно,
, следовательно,  – неявное задание функции.
– неявное задание функции. ,
,  .
. , (
, ( 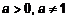 ).
). , (
, ( 

 Определение 11.
Определение 11.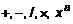 .
. .
. .
. ).
).