
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Этот пример показывает, что суперпозиция бинарных отношений, вообще говоря, не обладает свойством коммутативности.Доказательство. Поскольку
 ; ;   = =   = =  . .
Здесь EM – бинарное отношение равенства в множестве M. 5. Свойства суперпозиций бинарных отношений 1. Свойство объединения. Пусть во множестве A заданы бинарные отношения
Заметим, что в вышеприведенных соотношениях значки Доказательство. Пусть 2. Свойство ассоциативности. Для любых бинарных отношений
Доказательство. Пусть пара Это утверждение говорит о том, что какими бы двумя различными способами ни расставлять скобки в выражении 3) Суперпозиция обратных отношений. Определение 11. Пусть на множестве A задано бинарное отношение ПРИМЕР 7. Пусть на множестве A={0,1,2,3} задано бинарное отношение Для обратных отношений справедливы следующие равенства:
Заключение
 - отношение на множестве есть множество; - бинарные отношения могут быть заданы на декартовом произведении множеств; - отношения могут быть рефлексивными, симметричными, антисимметричными и транзитивными; - над отношениями можно делать такие же операции, как и над множествами; - суперпозиция определяет новое связное множество; - операция суперпозиции не коммутативна. Литература 1. Яблонский Я. В. Введение в дискретную математику. – М.: Высшая школа, 2001. - 384 с. 2. Москинова Г.И. «Дискретная математика». – М.: Логос, 2002. – 240 с. 3. Ильин В.А., Позняк Э.Г. «Л инейная алгебра». – М.: Физматлит, 2001. 4. Самсонов Б.Б. и др. «Компьютерная математика». – Ростов-на-Дону: Феникс, 2002. – 512 с.
Функции, заданные на множестве Понятие функции на множестве Мощность множеств Мощность континуума Цели занятия: изучить понятие функции на множестве, сопоставив его с уже известным понятием функции действительной переменной; научиться определять мощность множеств. Роль и место лекции Лекция посвящена понятию «функция». При изучении материала обычное представление о функции для общего случая любых множеств расширяется. Необходимо обратить внимание на общие черты между функцией на множестве и классической функцией и на связь между суперпозицией функций и суперпозицией отношений, обратным отношением и обратной функцией. 1. Понятие функции на множестве Введем понятие функции через бинарное отношение. Определение 1. Функцией называется любое бинарное отношение, которое не содержит двух пар с одинаковыми первыми элементами и разными вторыми. Если f – функция, то множество Df мы будем называть областью определения функции f, а множество Rf – областью значения функции. ПРИМЕР 1. 1. {(1,1); (2,3); (3,2)}, есть функция с областью определения {1,2,3} и это же множество является ее областью значений; 2. Бинарное отношение {(1, 2); (2, 2); (пешка, ферзь); (ладья, слон)} – есть функция с областью определения {1, 2, пешка, ладья} и областью значения {2, ферзь, слон}; 3. Бинарное отношение {(1,2); (1,1); (2,3)} не является функцией, поскольку содержит пары с одинаковыми первыми и разными вторыми элементами; 4. {((x, y), x+y) : (x,y)
 f, то элемент y называют значением функции f на x, или образом элемента x при f, поэтому элемент y мы будем обозначать f(x): y = f(x). Поскольку f – функция, то имеется только одна пара (x, y) с первой компонентой x и второй y, принадлежащая f. Достаточно часто говорят, что y является образом элемента x, а элемент x является прообразом элемента y. К функциям, поскольку они являются множествами, применимо понятие «равенство». f, то элемент y называют значением функции f на x, или образом элемента x при f, поэтому элемент y мы будем обозначать f(x): y = f(x). Поскольку f – функция, то имеется только одна пара (x, y) с первой компонентой x и второй y, принадлежащая f. Достаточно часто говорят, что y является образом элемента x, а элемент x является прообразом элемента y. К функциям, поскольку они являются множествами, применимо понятие «равенство».
Определение 2. Функции f и g равны между собой тогда и только тогда, когда они состоят из одних и тех же элементов:
Итак, пусть задана область определения функции f – множество Df. Часто возникает задача – найти область значений этой функции - множество Rf. Точно это сделать бывает трудно, поэтому иногда проще указать множество Y, такое, что Rf Определение 3. Если Df Определение 4. Если Df = X и Rf Определение 5. Если, кроме того, что Df = X, выполнено еще условие Rf = Y, то отображение (функцию) f называют отображением множества X "на" Y, или сюръекцией. Заметим, что каждая функция f является сюръекцией множества Df на Rf. Определение 6. Функция f называется инъективной, или инъекцией, если из того, что f(a) = f(b), следует, что a = b. Определение 7. Инъективное отображение множества X на множество Y называется однозначным (биективным), или просто биекцией типа X
1. Для заданной квадратичной функции f = {(x,y) 2. Рассмотрим функцию g, которая каждому элементу x В последнем примере было установлено взаимно-однозначное соответствие между множеством Z и его собственным подмножеством. Вообще говоря, справедливо следующее утверждение. Теорема 1. Множество M бесконечно тогда и только тогда, когда существует взаимно-однозначное соответствие между самим множеством M и его собственным подмножеством. Важно!!! Из определения суперпозиции бинарных отношений f и g следует, что когда f и g являются функциями, то значение их суперпозиции fg на элементе x вычисляется следующим образом: Определение 8. Когда для заданной функции f отношение f -1 является также функцией, то это отношение называется функцией обратной к f и обозначается f -1. Теорема 2. Для любой заданной функции f обратная ей функция f -1 существует тогда и только тогда, когда f – инъективна. Доказательство. Необходимость. Предположим, что для заданной функции f обратная к ней функция f -1 существует. Покажем, что в этом случае f – инъективна. Доказательство будем проводить от противного. Пусть f не является инъективным отображением. Это означает, что существует, по крайней мере, две пары (a, c)
В первой лекции говорилось о мощности конечных множеств, при этом мощностью конечного множества называлось число его элементов. Теперь перейдем теперь к множествам с бесконечным числом элементов. Как сравнивать такие множества априори непонятно - и в том и в другом множестве имеется бесконечно много элементов. Какая из двух бесконечностей больше? Поэтому, когда сравнивают бесконечные множества, обычно прибегают к такому трюку: пытаются построить отображение одного множества на другое, и если это удается, да еще отображение оказывается взаимно-однозначным, то множества объявляют "равными". Определение 9. Говорят, что множество A эквивалентно множеству B, если существует биективное отображение f: Под словами "биективное отображение" понимают взаимно-однозначное отображение "на". Эту биекцию записывают как A~B. ПРИМЕР 3. 1. Множество N и множество четных натуральных чисел эквивалентны. Необходимая биекция задается формулой f(n)=2n,
Определение 10.
Теорема 3. Два конечных множества имеют одинаковую мощность тогда и только тогда, когда они эквивалентны. Доказательство. Необходимость. Пусть два конечных множества имеют одинаковую мощность |A|=|B|= n, т.е. A = {a1, a2,..., an}, B = {b1, b2,..., bn}. Отображение f: A Достаточность. Пусть A~B и f: A Определение 11. Множество A называется счетным, если оно эквивалентно множеству натуральных чисел: A~N. В этом случае говорят, что множество A имеет счетную мощность. Теорема 4. Множество A имеет счетную мощность тогда и только тогда, когда элементы этого множества можно перенумеровать, используя все натуральные числа. Доказательство. Необходимость. Пусть множество A счетно. Это означает, что A~N. По определению эквивалентности существует биекция f: Достаточность. Пусть элементы множества A перенумерованы, т.е. A={a1,a2,...}. Определим отображение f: Теорема 5. Объединение конечного или счетного набора конечных или счетных множеств конечно или счетно. Теорема 6. Множество Q рациональных чисел счетно. Доказательство этого утверждения сводится к правилу пересчета всех рациональных чисел. Итак, мы познакомились с конечными и бесконечными множествами. Было показано, что надо понимать под мощностью множеств в каждом из рассмотренных случаев. Однако возникает вполне естественный вопрос – а существуют множества с мощностью большей, чем счетная? 3. Мощность континуума Теорема 7. Множество M = (0,1) несчетно.
Предположим, что множество M - счетно и, следовательно, элементы этого множества можно перенумеровать, используя все натуральные числа, т.е. M = {x1,x2,... }. Запишем числа
...
здесь
Множество A имеет мощность континуума, если оно эквивалентно множеству точек интервала (0,1). Мощность континуума обозначают буквой c. ПРИМЕР 4. Пусть a<b – два действительных числа. Покажем, что интервал (a,b) имеет мощность континуума. В качестве биекции, устанавливающей эквивалентность множеств (a,b) и (0,1), можно рассматривать функцию f(x) = (b-a)x+a: (0,1) Теорема 8. Существуют иррациональные числа. Более того, множество иррациональных чисел имеет мощность континуума. Доказательство. Поскольку Заключение В лекции заканчивается тема «Дискретная математика», однако на протяжении всего курса к ней необходимо будет возвращаться с целью расширения объема понятий и знаний. С целью лучшего восприятия остальных тем высшей математики объединим некоторые разделы дискретной математики с остальными темами. При этом нам придется столкнуться с такими разделами дискретной математики, как «Теория графов», «Логика», «Векторные пространства» и др. Важно целостное понимание всех разделов высшей математики на основе пройденного материала. Отметим следующее: - функция – это множество пар, у которых одному первому элементу соответствует единственный второй элемент; - как и у отношений, у функций есть обратная функция; - суперпозиция функции есть «сложная функция» в классическом понимании; - бесконечные множества имеют мощность; - мощность Литература 1. Яблонский Я. В. Введение в дискретную математику. – М.: Высшая школа, 2001. – 384 с. 2. Москинова Г.И. Дискретная математика. – М.: Логос, 2002. – 240 с. 3. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Физматлит, 2001. 4. Самсонов Б.Б. и др. Компьютерная математика. – Ростов-на-Дону: Феникс, 2002. – 512 с.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 847. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  , получаем, что пара
, получаем, что пара 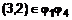 . Теперь надо показать, что пара
. Теперь надо показать, что пара  . Перепишем бинарное отношение
. Перепишем бинарное отношение  как
как  . Следовательно,
. Следовательно,  , причем для любого n, откуда получаем, что пара
, причем для любого n, откуда получаем, что пара  , что невозможно. Однако легко показать, что
, что невозможно. Однако легко показать, что и
и  ,
,  I. Здесь I - конечный или бесконечный набор индексов. Тогда
I. Здесь I - конечный или бесконечный набор индексов. Тогда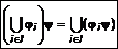 ,
,  . (2)
. (2) нельзя заменить на
нельзя заменить на  .
.
 и
и 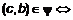

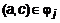


 .
. , заданных на некотором множестве A, справедливо равенство:
, заданных на некотором множестве A, справедливо равенство: . (3)
. (3)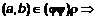
 и
и  . Это означает, что
. Это означает, что  и
и 
 и
и  . Итак, мы доказали, что если
. Итак, мы доказали, что если 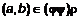 , то из этого следует, что
, то из этого следует, что 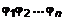 , чтобы получить суперпозицию двух отношений, получим равные отношения.
, чтобы получить суперпозицию двух отношений, получим равные отношения. , также заданное на A, которое состоит из тех и только тех пар
, также заданное на A, которое состоит из тех и только тех пар  , для которых справедливо, что
, для которых справедливо, что  .
.  ={(0,1); (2,3); (1,3)}, тогда
={(0,1); (2,3); (1,3)}, тогда  = {(1,0); (3,2); (3,1)}.
= {(1,0); (3,2); (3,1)}. ,
,  . (4)
. (4)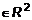 } - функция с областью определения в
} - функция с областью определения в  и областью значений в
и областью значений в  и
и  .
. Y. Удобно ввести следующие определения.
Y. Удобно ввести следующие определения. Y.
Y.  . Для проверки биективности функции f необходимо проверить, является ли она еще и инъекцией. Квадратичная функция f такова, что f(1) = f(-1), однако отсюда не следует, что 1 = -1. Таким образом, показали, что отображение f не является инъекцией. Следовательно, биективным такое отображение f также не является.
. Для проверки биективности функции f необходимо проверить, является ли она еще и инъекцией. Квадратичная функция f такова, что f(1) = f(-1), однако отсюда не следует, что 1 = -1. Таким образом, показали, что отображение f не является инъекцией. Следовательно, биективным такое отображение f также не является.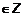 ставит в соответствие число g(x) = 2x+1. Покажем, что заданная таким образом функция g является взаимно-однозначным соответствием между Z и множеством нечетных целых чисел. Действительно, из того, что 2x1+1 = 2x2+1, следует, что x1 = x2.
ставит в соответствие число g(x) = 2x+1. Покажем, что заданная таким образом функция g является взаимно-однозначным соответствием между Z и множеством нечетных целых чисел. Действительно, из того, что 2x1+1 = 2x2+1, следует, что x1 = x2.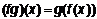 – и означает, что если f:
– и означает, что если f: 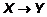 , а g:
, а g:  , тогда fg :
, тогда fg :  .
.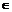 f, (b, c)
f, (b, c)  . Следовательно, f -1 содержит пары (c, a), (c, b) и поскольку
. Следовательно, f -1 содержит пары (c, a), (c, b) и поскольку  (см.: Л.3, опр.4).
(см.: Л.3, опр.4). .
. 2. Множества (0,1) и R эквивалентны. Этот пример немного неожиданен, поскольку утверждается, что число точек открытого интервала (0,1) равно числу точек всей вещественной прямой. Нужная нам биекция строится следующим образом (рис. 1). Представим интервал (-1,1) в виде некоторой полуокружности. Множество действительных чисел представим некоторой прямой. Из центра полуокружности проведем любую прямую линию в некоторую точку (mi) на прямой R. Очевидно, что прямые линии, соединяют единственную точку
2. Множества (0,1) и R эквивалентны. Этот пример немного неожиданен, поскольку утверждается, что число точек открытого интервала (0,1) равно числу точек всей вещественной прямой. Нужная нам биекция строится следующим образом (рис. 1). Представим интервал (-1,1) в виде некоторой полуокружности. Множество действительных чисел представим некоторой прямой. Из центра полуокружности проведем любую прямую линию в некоторую точку (mi) на прямой R. Очевидно, что прямые линии, соединяют единственную точку 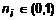 на полуокружности с единственной точкой
на полуокружности с единственной точкой  вещественной прямой и задают биекцию между точками интервала (0,1) и точками всей прямой, являющейся множеством R.
вещественной прямой и задают биекцию между точками интервала (0,1) и точками всей прямой, являющейся множеством R.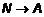 . Положим, что an= f(n),
. Положим, что an= f(n),  в виде десятичных дробей (без 9 в периоде):
в виде десятичных дробей (без 9 в периоде):


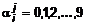 ; верхний индекс обозначает номер числа, а нижний – порядковый номер знака. Теперь образуем новое число
; верхний индекс обозначает номер числа, а нижний – порядковый номер знака. Теперь образуем новое число  по следующему правилу:
по следующему правилу:  , если
, если  , и 0, если
, и 0, если  . Тогда очевидно, что
. Тогда очевидно, что  , но образованное таким образом новое число не совпадает ни с одним из пересчитанных чисел xi. Следовательно, интервал (0,1) содержит, как минимум, на 1 точку больше, чем есть натуральных чисел, и его мощность не равна мощности множества натуральных чисел. Мы доказали, что множество точек интервала (0,1) не счетно.
, но образованное таким образом новое число не совпадает ни с одним из пересчитанных чисел xi. Следовательно, интервал (0,1) содержит, как минимум, на 1 точку больше, чем есть натуральных чисел, и его мощность не равна мощности множества натуральных чисел. Мы доказали, что множество точек интервала (0,1) не счетно. (a,b).
(a,b).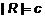 и
и  , а
, а  , мы получаем, что
, мы получаем, что  .
.