
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Операции над бинарными отношениямиСуперпозиция бинарных отношений Свойства суперпозиций бинарных отношений Цели занятия: изучить понятие отношения на множестве как его некоторые подмножества; научиться осуществлять операции над отношениями; понять принцип суперпозиции отношений. Роль и место лекции На предыдущих лекциях мы познакомились с основными терминами и операциями над множествами. Из школьного курса математики известно понятие функции, как некоторой зависимости между действительными элементами области определения и действительными значениями области значений. В этой лекции станет понятным, что это лишь частный случай. Понятие функции более широкое. Кроме того, в последующих лекциях по линейной алгебре и теории аналитических функций будут рассматриваться с точки зрения множеств такие важные понятия как «оператор» и «функционал». Следует обратить внимание на понятия «суперпозиция» и «обратное отношение», которые непосредственно связаны с уже известными вам понятиями сложной и обратной функции действительного переменного. Именно знания по дискретной математике позволяют понимать и «чувствовать» математику на более высоком уровне. 1. Отношения на множествах Определение 1. Отношение – это один из способов задания взаимосвязей между элементами множеств. Они бывают унарные, бинарные и в общем случае n-арные. Определение 2. Унарные (одноместные) отношения на множестве – это наличие какого-то определенного признака R (свойства и т. п.) у элементов a некоторого множества M. Унарное отношение образует некоторое подмножество на множестве, в котором они введены, т. е. 
Множество животных одного вида являются подмножеством множества рода животных и т. д. Так {грызуны} Определение 3. Соответствие – это способ задания взаимосвязей, взаимодействий между элементами множества (наряду с отношениями). Частными случаями соответствия являются функции, операции, преобразования и др. Определение 4. Два множества называются эквивалентными, если для любого элемента а множества А найдется такой элемент b множества В, что 2. Бинарные отношения Определение 5. Бинарное (двухместное) отношение на множестве – это наличие каких-либо взаимосвязей R, которыми характеризуются пары элементов на некотором множестве M. Тогда все пары Определение 6. Сокращенное определение. Говорят, что на множестве M задано бинарное отношение Другими словами, бинарное отношение на множестве M – это подмножество в M×M. Утверждение, что элемент a состоит в отношении
ПРИМЕР 2. 1. Отношение делимости в N. Число n состоит в этом отношении с числом m, если n делится на m {(1,1),(3,6),(3,9)…}:. Подмножество R в N2, определяющее отношение делимости, имеет вид: R = {(n,m) 2. Отношение " 3. Отношение равенства в R. Числа x и y состоят в этом отношении, если они равны {(1,1),(3,3)…}: R = {(x,y) 4. Отношение {семейной пары} на множестве {люди}. Определение 7. Бинарное отношение - рефлексивным, если a - симметричным, если a - антисимметричным, если (a - транзитивным, если (a ПРИМЕР 3.
 ", заданное на множестве R, является рефлексивным, однако отношение "<", заданное на том же самом множестве R, не рефлексивно. Докажем второе утверждение. Бинарное отношение " < " это: ", заданное на множестве R, является рефлексивным, однако отношение "<", заданное на том же самом множестве R, не рефлексивно. Докажем второе утверждение. Бинарное отношение " < " это:
"<"=R = {(x,y) означающее, что произвольный элемент 2. Определим на множестве R следующее бинарное отношение: элементы [x] = [y] Определение 8. Бинарное отношение
Пусть на множестве M={1, 2, 3} задано бинарное отношение 1. Необходимо проверить, что для любого элемента a из множества M пара (a,a) принадлежит бинарному отношению 2. Выполнение условия 3. Должно выполняться свойство: Действительно: 3. Операции над бинарными отношениями Мы уже знаем, что бинарные отношения являются множествами, и, следовательно, можно говорить о равенстве бинарных отношений и о включении одного бинарного отношения в другое: - - - - ПРИМЕР 5. Определим следующие бинарные отношения:
тогда между ними имеют место следующие отношения включения: В биологии отношение на множестве {ареал} может определять подмножество {вид животных}. 4. Суперпозиция бинарных отношений Определение 9.
 и и  называется бинарное отношение (будем обозначать его как называется бинарное отношение (будем обозначать его как  ), определенное следующим образом: ), определенное следующим образом:  когда в множестве A найдется хотя бы один элемент b, такой, что когда в множестве A найдется хотя бы один элемент b, такой, что  и и  . .
Определение 10. Множество называется связным, если на этом множестве можно определить суперпозицию любых подмножеств. ПРИМЕР 6. Для бинарных отношений, определенных в предыдущем примере, нужно показать, что справедливы следующие равенства: 1. 2. 3. Замечание!!! |
||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 7016. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. {млекопитающие} подмножество задано отношением «класс»
{млекопитающие} подмножество задано отношением «класс» .
.  элементов из М, между которыми имеет место данное отношение R,образуют подмножество пар из множества всех возможных пар элементов
элементов из М, между которыми имеет место данное отношение R,образуют подмножество пар из множества всех возможных пар элементов  , т. е.
, т. е.  , при этом
, при этом  .
. .
. , или
, или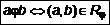 . (1)
. (1) :
:  : n = km}.
: n = km}.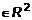 : x
: x  a
a 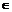 M,
M, 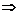 b
b  a
a  : x<y},
: x<y},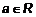 должен удовлетворять неравенству a < a, а это неправда. Следовательно, произвольный элемент a не состоит сам с собой в отношении "<", и рефлексивности нет. Множество {животные одного вида} рефлексивно.
должен удовлетворять неравенству a < a, а это неправда. Следовательно, произвольный элемент a не состоит сам с собой в отношении "<", и рефлексивности нет. Множество {животные одного вида} рефлексивно. связаны бинарным отношением
связаны бинарным отношением  ={(1,2); (2,1); (1,1); (2,2); (3,3)}. Доказать, что заданное таким образом бинарное отношение
={(1,2); (2,1); (1,1); (2,2); (3,3)}. Доказать, что заданное таким образом бинарное отношение  видно прямо из определения бинарного отношения
видно прямо из определения бинарного отношения  .
.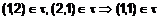 ,
,  и т. д.
и т. д. . На бинарные отношения, заданные на некотором множестве переносятся общие операции над множествами. Пусть
. На бинарные отношения, заданные на некотором множестве переносятся общие операции над множествами. Пусть  – бинарное отношение в A, пересечение отношений
– бинарное отношение в A, пересечение отношений  – бинарное отношение в A, объединение отношений
– бинарное отношение в A, объединение отношений 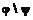 – бинарное отношение в A, разность отношений
– бинарное отношение в A, разность отношений 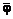 – бинарное отношение в A, дополнение к бинарному отношению
– бинарное отношение в A, дополнение к бинарному отношению  .
. 



 ;
;  ;
;  ;
;  . Последнее бинарное отношение является отношением равенства в Z и т.д.
. Последнее бинарное отношение является отношением равенства в Z и т.д. =
=  . Действительно, поскольку
. Действительно, поскольку  ,
,  , то
, то  ; обратно, если
; обратно, если  ,
,  , то
, то  =
=  . Рассмотрим произвольную пару
. Рассмотрим произвольную пару 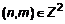 , возможны два случая a)
, возможны два случая a) 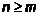 ; b)
; b) 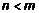 . Рассмотрим случай a)
. Рассмотрим случай a) 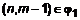 ,
, 
 . В случае b)
. В случае b)  ,
, 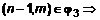
 и, следовательно,
и, следовательно,  ;
;
 .
.