
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Само множество может быть элементом другого множества.2. Подмножество Определение 8. Пусть A и B – какие-то два множества. Если любой элемент x множества A является элементом множества B, то говорят, что множество A является подмножеством множества B и обозначают этот факт как Это же определение можно переписать на языке сокращений:
Читается оно так: "Если элемент x принадлежит множеству A, то x принадлежит множеству B". Из введенного определения, очевидно, следует утверждение, если Замечание!!! Пустое множество Определение 9. Подмножество A множества B, отличное от самого множества B и Это так называемое "строгое" включение множества A в множество B. ПРИМЕР 6.
3. Свойства включений 1) 2) 3) Определение 10. Подмножества B и Вывод!!!
ПРИМЕР 7. Всевозможные подмножества множества A={a,b} суть Заключение В лекции начато изучение высшей математики. Введено важное понятие множества. Важно понять, что множество – это совокупность элементов. Одно множество может быть элементом другого множества, поэтому, рассматривая какие-либо математические операции, действия, графики и т. д., важно определиться, каким множеством мы оперируем, иначе все выводы нельзя принять верными.  Отметим следующее: - множество есть многое, мыслимое нами как целое; - само множество может быть элементом другого множества; - для быстроты и простоты записи используют сокращения; - пустое множество единственное; - в равных множествах последовательность элементов не важна; - важно различать Литература 1. Москинова Г.И. Дискретная математика. – М.: Логос, 2002. – 240 с. 2. Яблонский Я. В. Введение в дискретную математику. – М.: Высшая школа, 2001, - 384 с. 3. Шипачев В.С. Основы высшей математики. - М.: Высшая школа,1998. 4. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989, - 659 с.
Алгебра множеств Операции над множествами. Диаграммы Венна Принцип двойственности Декартово произведение множеств Цели занятия: на базе полученных знаний изучить операции над множествами; научиться абстрагировать множества диаграммами Венна и осуществлять операции над ними; изучить понятие «декартово произведение». Роль и место лекции В этой лекции мы рассмотрим некоторые способы получения новых множеств из уже имеющихся. Эти способы обычно называются операциями над множествами. Основные свойства этих операций и связи между ними принято называть алгеброй множеств. Понимание операций над множествами позволит шире взглянуть на уже известные математические операции и обобщить их, т. е. непосредственно подойти к таким понятиям высшей математики как «оператор», «функционал» и др. Обратите внимание на последний и такое, казалось бы, глобальное известное математическое понятие, как «декартова плоскость», окажется частным случаем. А понимание универсального множества будет важно при изучении бесконечно малых и бесконечно больших величин. Поэтому отмечаем особую важность первых лекций. 1. Операции над множествами. Диаграммы Венна Объединение и пересечение Определение 1. Объединением (суммой) двух множеств A и B называется множество (его принято обозначать
ПРИМЕР 1. Рассмотрим множества A = {1, 2, 3, 4}, B = {1,3,5}, C = {5,6}. Тогда согласно введенному определению получаем:
 {Камышовая кошка} {Камышовая кошка}  … = {Род кошек}. … = {Род кошек}.
Аналогично определяется объединение (сумма) n
Определение 2. Пересечением (произведением) двух множеств A и B называется множество (его принято обозначать
ПРИМЕР 2. В рамках введенных в предыдущем примере определений множеств A, B, C мы получаем:
Так же как мы делали раньше, можно определить пересечение (произведение) конечного числа множеств. На кругах Эйлера пересечение множеств представлено на рис. 2.
1. Коммутативности:
2. Ассоциативности:
Справедливость этих свойств следует из самих определений операций пересечения и объединения множеств, поэтому обычно скобки в таких групповых операциях опускают. 3. Закон взаимной дистрибутивности:
Разность множеств Определение 3.
На кругах Эйлера выражение (3) представлено на рис. 3. ПРИМЕР 3. В рамках введенных в примере 1 определений множеств A, B, C справедливы следующие результаты A \ B = {2,4}; B \ C = {1,3}; A \ C = A. Определение 4.
На кругах Эйлера выражение (4) представлено на рис. 4. ПРИМЕР 4. В рамках введенных в примере 1 определений множеств A, B, C справедливы следующие результаты:
 ; ;
Свойства разности множеств 1. Разности: A \ B = A \ (A Важно!!! Операция разности определяется только для двух множеств. Эта операция двухместная и не коммутативная: 2. Свойство симметрической разности:
Доказательство. Доказательство этого свойства, как и других утверждений о равенстве каких-либо множеств, состоит в том, чтобы, предположив принадлежность некоторого элемента x множеству из левой части равенства, доказать, что этот же самый элемент принадлежит множеству, стоящему в правой части равенства и наоборот. Пусть Итак, мы доказали, что если некоторый элемент x принадлежит множеству из левой части равенства, то из этого следует, что он принадлежит множеству, стоящему в правой части равенства. Теперь нам необходимо доказать обратное включение. Пусть x Важно!!! Итак, мы полностью доказали заявленное свойство. При доказательстве подобных утверждений огромную роль играет то свойство, что если некоторый элемент x принадлежит некоторому множеству X, то он, очевидно, будет принадлежать и объединению множества X с произвольным другим множеством. Определение 5. Множество U, такое, что все рассматриваемые множества являются его подмножествами, называется универсальным.
ПРИМЕР 5. Множества {звездные скопления}, {черные дыры}, {планеты} являются подмножествами универсального множества {вселенная}. Определение 6. Множество U \ A называется дополнением множества A (до универсального множества) и обозначается через На кругах Эйлера это определение представлено на рис. 5. Принцип двойственности Теорема двойственности Теорема 1 (двойственности или де-Моргана). Пусть Ak, k = 1,..., n – некоторые подмножества универсального множества U, тогда имеют место следующие равенства:
Эти равенства, связывающие операции пересечения и объединения множеств и их дополнений до универсального множества, называют соотношениями принципа двойственности. Доказательство.
Заметим, что в приведенном доказательстве все утверждения об элементе x соединены знаками ПРИМЕР 6.
 . .
Решение. 1.
2. Каждое натуральное число является либо четным, либо нечетным, поэтому 3.
4. A Базис операций Если теперь считать, что в нашем распоряжении имеется универсальное множество U, то операции ПРИМЕР 7. 1. 2. 3. Определение 7. Операции { 3. Декартово произведение множеств В математике достаточно часто приходится иметь дело не только с отдельными элементами какого-либо множества, но и с упорядоченными парами его элементов. Примерами упорядоченных пар могут служить (a, b), (1, 1). В упорядоченных парах числа могут совпадать, а могут и не совпадать. Аналогично сказанному можно ввести в рассмотрение упорядоченные тройки, упорядоченные четверки, а в общем случае и упорядоченные наборы длины n элементов данного множества. Набор, составленный из элементов a1, a2, ... an, n = 2,3,... взятых именно в этом порядке, будем обозначать (a1,..., an) и говорить, что i-я компонента этого набора есть ai. Длиной набора (a1,..., an) будем называть число n его компонент. Определение 8. Два набора равны между собой, т. е. (a1,...,an) = (b1,...,bn), тогда и только тогда, когда для любого i выполнено равенство ai=bi. ПРИМЕР 8. (a, a, b) Условимся называть элемент a некоторого множества A набором длины один, тогда можно ввести пустой набор - набор длины нуль, который мы будем обозначать Определение 9. Декартовым (прямым) произведением множеств A1,..., An (n
Через
Рассмотрим два множества A1 = [0, 1], A2 = [2, 3]. Если на плоскости выбрать некоторую декартову систему координат, то прямое произведение A1×A2 можно представить как квадрат со стороной длины 1 (рис. 6).
 . В дальнейшем при изучении функций двух переменных, в отличие от функции одной переменной, нам потребуется находить область определения как некоторую часть декартовой плоскости. В этом случае диаграммы Венна получат большую наглядность и будут представлены кривыми второго порядка. . В дальнейшем при изучении функций двух переменных, в отличие от функции одной переменной, нам потребуется находить область определения как некоторую часть декартовой плоскости. В этом случае диаграммы Венна получат большую наглядность и будут представлены кривыми второго порядка.
Заключение В лекции изучены важные операции над множествами «объединение», «пересечение», «разность». Познакомились с новым «универсальным» множеством. Полученные знания будут необходимы при изучении темы «Отношения множеств». Отметим следующее: - операции объединения и пересечения коммутативны; - операция разности не коммутативна; -
- универсальное множество содержит все множества; - доказательство теорем осуществляется на основе принадлежности элемента множества, как к левой, так и правой части; - если элемент принадлежит множеству, то он принадлежит и объединению этого множества с любым другим множеством; - декартовым произведением множеств называется новое множество, элементами которого являются пары, составленные из элементов исходных множеств; - Декартова плоскость это множество Литература 1. Яблонский Я. В. Введение в дискретную математику. – М.: Высшая школа, 2001. - 384 с. 2. Москинова Г.И. Дискретная математика. – М.: Логос, 2002. – 240 с. 3. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Физматлит, 2001. 4. Самсонов Б.Б. и др. Компьютерная математика. – Ростов-на-Дону: Феникс, 2002. – 512 с. 5. Демидович Б.П, Кудрявцев В.А.. Краткий курс высшей математики. – М.: Наука, 2001. - 656 с. Лекция 3 Отношения
Бинарные отношения |
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 570. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 или
или 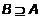 .
. .
.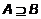 , то A=B, т.е. множества A и B состоят из одних и тех же элементов.
, то A=B, т.е. множества A и B состоят из одних и тех же элементов. по определению считается подмножеством любого множества, т. е.
по определению считается подмножеством любого множества, т. е. 
 A.
A. .
.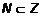 ,
, 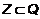 . Однако интервалы [1,2] и (1,3] не удовлетворяют никаким условиям включения. В каждом из этих множеств есть элементы, не принадлежащие другому множеству.
. Однако интервалы [1,2] и (1,3] не удовлетворяют никаким условиям включения. В каждом из этих множеств есть элементы, не принадлежащие другому множеству.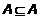 ;
; A=B;
A=B;
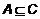 .
. , {a}, {b}, {a,b}, из которых {a}, {b} – собственные подмножества множества A.
, {a}, {b}, {a,b}, из которых {a}, {b} – собственные подмножества множества A. – собственное подмножество.
– собственное подмножество. ), состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств - либо A, либо B
), состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств - либо A, либо B . (1)
. (1) = {1, 2, 3, 4, 5};
= {1, 2, 3, 4, 5};  = {1, 2, 3, 4, 5, 6}.
= {1, 2, 3, 4, 5, 6}. 2 множеств A1,A2, ..., An. Объединением этих множеств называется множество, обозначаемое A1
2 множеств A1,A2, ..., An. Объединением этих множеств называется множество, обозначаемое A1  Достаточно часто для наглядного изображения этих операций над множествами используют так называемые круги Эйлера (диаграммы Венна). Множества при таком подходе изображают кругами, а результат операции закрашивают или заштриховывают. Результат операции объединения двух множеств представлен на рис. 1.
Достаточно часто для наглядного изображения этих операций над множествами используют так называемые круги Эйлера (диаграммы Венна). Множества при таком подходе изображают кругами, а результат операции закрашивают или заштриховывают. Результат операции объединения двух множеств представлен на рис. 1.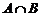 ), состоящее из всех тех и только тех элементов, которые принадлежат каждому из множеств A и B
), состоящее из всех тех и только тех элементов, которые принадлежат каждому из множеств A и B . (2)
. (2) ,
,  ,
, 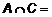
 В биологии пересечение множеств может определять среду обитания или произрастания. Например {Редкие растения}
В биологии пересечение множеств может определять среду обитания или произрастания. Например {Редкие растения}  {Растения края} = {Заповедник}.
{Растения края} = {Заповедник}. ;
;  .
. ;
;  .
. ;
;  .
. Разностью двух множеств A и B называется множество (его обычно обозначают A\B или A-B), состоящее из тех и только тех элементов, которые принадлежат множеству A и не принадлежат множеству B .
Разностью двух множеств A и B называется множество (его обычно обозначают A\B или A-B), состоящее из тех и только тех элементов, которые принадлежат множеству A и не принадлежат множеству B . . (3)
. (3) Симметрической разностью множеств A и B называется множество, обозначаемое через A
Симметрической разностью множеств A и B называется множество, обозначаемое через A  B и определяемое следующим образом:
B и определяемое следующим образом: . (4)
. (4) , поскольку
, поскольку  =
=  B) и A \ (B
B) и A \ (B  .
.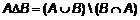
 .
. , что по определению симметрической разности означает, что x
, что по определению симметрической разности означает, что x 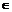 (A\B)
(A\B)  B)
B)  B и x
B и x  . Ситуация, когда x
. Ситуация, когда x 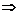 (x
(x  и
и  , либо
, либо  и
и  . Рассмотрим первый случай: пусть
. Рассмотрим первый случай: пусть  и
и  . Откуда
. Откуда  .Второй случай доказывается аналогично.
.Второй случай доказывается аналогично. То есть это множество, которое по предположению содержит все используемые нами множества. Обозначается не кругом, а прямоугольником (рис. 5).
То есть это множество, которое по предположению содержит все используемые нами множества. Обозначается не кругом, а прямоугольником (рис. 5).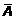 .
. ;
;  . (5)
. (5) .
. , что позволяет одновременно строить доказательство утверждения в обе стороны.
, что позволяет одновременно строить доказательство утверждения в обе стороны. – это множество нечетных натуральных чисел, т.е. множество B.
– это множество нечетных натуральных чисел, т.е. множество B.
 =
=  =
= 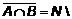
 10} = {2, 4, 6, 8, 10}.
10} = {2, 4, 6, 8, 10}. можно определять друг через друга и фактически ввести некоторый базис операций в алгебре множеств.
можно определять друг через друга и фактически ввести некоторый базис операций в алгебре множеств. .
. .
.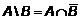 .
. (a, b, a); (a, 2)
(a, b, a); (a, 2)  .
. .
. обозначают декартово произведение n – штук множеств M. Его элементами являются упорядоченные наборы из n элементов, каждый из которых принадлежит множеству M. Множество
обозначают декартово произведение n – штук множеств M. Его элементами являются упорядоченные наборы из n элементов, каждый из которых принадлежит множеству M. Множество  ,
,  =
=  ПРИМЕР 9.
ПРИМЕР 9.