
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Скалярное произведение в трехмерном пространствеСкалярное произведение векторов Угол между векторами; направляющие косинус векторы Цели занятия:познакомиться с понятием эвклидова пространства; на основе предыдущей лекции рассмотреть эвклидово пространство как частный случай; понять смысл скалярного произведения; научиться определять скалярное произведение векторов, представленных в различных видах. Роль и место лекции. Полученные знания будут необходимы для восприятия темы «Векторный анализ, элементы теории поля». Такое фундаментальное понятие, как «скалярное произведение» позволит взглянуть на понятие пространства с другой стороны и осознать, что эвклидово пространство – это некоторая часть нашего мира, удовлетворяющая лишь определенным условиям. На основе этого пространства формируются аксиомы. В другом пространстве может формироваться новая математика. 1. Понятие «эвклидово пространство» Возьмем трехмерное линейное пространство L= Определение 1. Скалярным произведением двух элементов Обозначается скалярное произведение как Возьмем n-мерное линейное пространство
Скалярным произведением векторов Проверим, удовлетворяет ли (2) определению 1. 1) 2) 3) 4) Аналогичным образом необходимо проверять любые функционалы, претендующие на скалярное произведение. Возьмем пространство  Определение 3. Скалярным произведением функций
Удовлетворяет ли выражение (2) условиям (1) предлагается проверить самостоятельно. Определение 4. Пространство, в котором определено скалярное произведение, называется эвклидовым, т. е. Теорема 1. Всякое эвклидово пространство нормировано. Доказательство. Норма в эвклидовом пространстве задается как
1) 2) 3) 1. 2. Для проверки второго условия воспользуемся неравенством Коши-Буняковского: С учетом второго условия и (4) рассмотрим норму суммы:
3. Все три условия выполняются. Теорема доказана. 2. Скалярное произведение в трехмерном пространстве Возьмем два вектора Определение 5. Скалярным произведением векторов в С учетом равенства Покажем, что (5) также удовлетворяет условиям (1): 1) 2) 3) 4) ПРИМЕР 1.
 под углом под углом  к поверхности прямолинейно к поверхности прямолинейно  перемещено тело. При этом работа, выполненная силой, будет равна произведению длины пути на произведение модуля силы и косинуса угла перемещено тело. При этом работа, выполненная силой, будет равна произведению длины пути на произведение модуля силы и косинуса угла  (рис. 1). Так как. (рис. 1). Так как.  , то , то 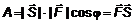 . Работа есть скалярное произведение векторов силы и пути. . Работа есть скалярное произведение векторов силы и пути.
Теорема 2. Два вектора перпендикулярны Доказательство. Необходимость. Дано Из определения 5 следует, что Достаточность. Дано Вывод!!! 3. Скалярное произведение векторов Возьмем два вектора в Скалярное произведение этих векторов
Возьмем два вектора в
Определение 6. Направляющим называется косинус угла между вектором и одним из базисных векторов. Единичный вектор может быть задан как Заключение В лекции рассматривалось эвклидово пространство, математический и физический смысл скалярного произведения; изучено понятие «направляющий косинус». Отметим: - в эвклидовом пространстве пространство должно быть задано скалярное произведение; - скалярное произведение есть число; - два вектора перпендикулярны, если их скалярное произведение равно 0; - угол между векторами определяется их скалярным произведением и длинами векторов; - единичный вектор можно задавать направляющими косинусами. Литература 1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001. 2. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.
Определители, векторные и |
||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 503. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. и
и  пространства L называется функционал
пространства L называется функционал 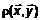 , удовлетворяющий определенным свойствам:
, удовлетворяющий определенным свойствам: . (1).
. (1). или
или  .
. , в котором заданы два вектора
, в котором заданы два вектора  и
и 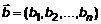 .
. и
и  называется число, равное сумме попарных произведений соответствующих координат этих векторов.
называется число, равное сумме попарных произведений соответствующих координат этих векторов.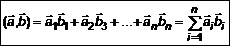 . (2)
. (2)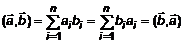 ;
; ;
; ;
; .
.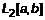 - квадрат интегрируемых функций
- квадрат интегрируемых функций и
и 
 называется интеграл произведения этих функций на отрезке
называется интеграл произведения этих функций на отрезке 
 . (3)
. (3)
 ;
; ;
; .
. , следовательно,
, следовательно,  .
.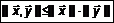 . (4)
. (4)
 .
. =
=  =
= 
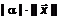 .
. ,
, 
 .
. , где
, где 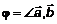 . (5)
. (5) запишем выражение (5)
запишем выражение (5)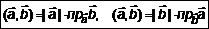 . (6)
. (6) ;
;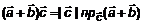 =(теорема 5, л. 2)=
=(теорема 5, л. 2)=  =
= 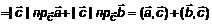 ;
; ;
;
 .
.
 , когда их скалярное произведение было равно нулю.
, когда их скалярное произведение было равно нулю.  .
. . Доказать, что
. Доказать, что  .
.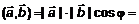 =
= 
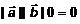 , следовательно,
, следовательно,  . Тогда
. Тогда  или
или  , или
, или 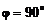 . Поскольку рассматриваем не нулевые векторы, то
. Поскольку рассматриваем не нулевые векторы, то  перпендикулярен любому вектору.
перпендикулярен любому вектору. ,
,  .
.


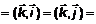
 , т. к. это базисные векторы и
, т. к. это базисные векторы и 
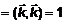 , так как
, так как  . Поэтому
. Поэтому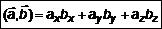 . (7)
. (7) ,
,  . Из (5)
. Из (5) 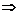
 . (8)
. (8) Найдем углы между вектором
Найдем углы между вектором  . То есть
. То есть  ,
,  ,
,  (рис. 2).
(рис. 2).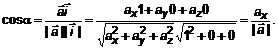 Аналогично найдем остальные косинусы
Аналогично найдем остальные косинусы . (9)
. (9) .
.