
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ КОРПУСА РАКЕТЫ(продольные) Продольные колебания ракеты с ЖРД - это колебания замкнутой системы, основными физическими звеньями которой являются корпус ракеты, двигатель и топливоподающие магистрали. Если из замкнутой системы выделить одно звено, в данном случае корпус ракеты, то можно рассмотреть его вынужденные колебания под действием отклонения тяги двигателя. Рассмотрим вынужденные колебания корпуса ракеты, схемой которой является неоднородный стержень с упругоподвешенными сосредоточенными массами различной величины. Уравнение вынужденных продольных колебаний корпуса ракеты можно представить в виде
где
Сосредоточенная сила
где Перемещение стержня
Здесь
При Введем функцию
и следующее правило интегрирования функции:
Теперь с учетом всех выше изложенных зависимостей уравнение
можно представить в таком виде:
При
Функции 
ортогональны с весовой функцией Условие ортогональности можно представить в виде
Будем считать функций
вместо
Проинтегрируем это уравнение по
получим следующую систему обыкновенных дифференциальных уравнений для определения обобщенных координат
где
Несмотря на сложность колебательной системы, такая простая структура уравнений
достигается потому, что собственные формы и частоты колебаний определены для корпуса с учетом колебаний жидкости в упругих баках как единой колебательной системы. Вынужденные продольные колебания ракеты могут происходить под воздействием внешних сил - отклонения тяги двигателя и отклонения аэродинамической силы лобового сопротивления. Отклонение тяги двигателя оказывает значительно большее влияние на продольные колебания корпуса ракеты, чем отклонение силы лобового сопротивления. Поэтому в практических расчетах отклонение силы лобового сопротивления обычно не учитывают. Когда расходную магистраль выделяют в отдельное звено, отклонение давления жидкости перед входом в насос также будет создавать внешнюю силу по отношению к корпусу. На корпус ракеты эта сила передается через подвеску насоса (двигателя). Для уравнения
Для второго уравнения
где Знак минус перед силой
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 723. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
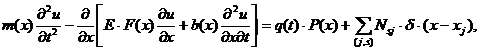
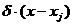 - функция Дирака, обладающая следующим свойством:
- функция Дирака, обладающая следующим свойством: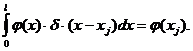
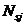 , передаваемая стержню через пружину, численно равна силе инерции массы
, передаваемая стержню через пружину, численно равна силе инерции массы 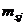 :
: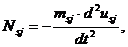
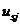 - перемещение массы
- перемещение массы 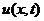 при вынужденных колебаниях представим в виде разложения в ряд по формам собственных колебаний:
при вынужденных колебаниях представим в виде разложения в ряд по формам собственных колебаний: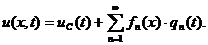
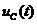 - перемещение центра масс системы;
- перемещение центра масс системы; 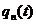 - обобщенная координата упругих колебаний;
- обобщенная координата упругих колебаний; 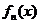 - собственная форма колебаний n-го тона стержня с упругоподвешенными сосредоточенными массами
- собственная форма колебаний n-го тона стержня с упругоподвешенными сосредоточенными массами
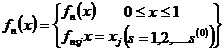
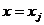 функция
функция 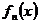 будет многозначной со значениями
будет многозначной со значениями 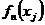 ,
, 
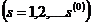 . Для всех остальных
. Для всех остальных 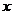 эта функция будет иметь одно значение
эта функция будет иметь одно значение 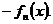 .
.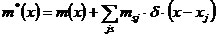
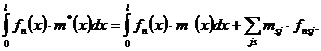
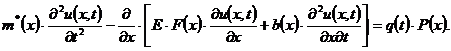
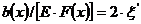 и
и 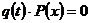 переменные в уравнении
переменные в уравнении 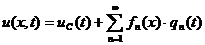 можно разделить и получить уравнение для определения собственных форм и частот колебаний:
можно разделить и получить уравнение для определения собственных форм и частот колебаний: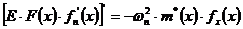
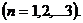
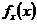 , удовлетворяющие этому уравнению и граничным условиям
, удовлетворяющие этому уравнению и граничным условиям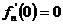 ;
; 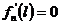 ,
,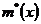 .
.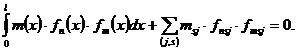
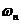 известными и перейдем к рассмотрению задачи о вынужденных колебаниях. Подставив в уравнение
известными и перейдем к рассмотрению задачи о вынужденных колебаниях. Подставив в уравнение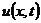 его выражение из уравнения
его выражение из уравнения 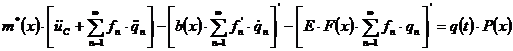 .
.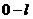 . Затем умножим уравнение на
. Затем умножим уравнение на 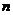 - произвольное фиксированное число, и проинтегрируем его по
- произвольное фиксированное число, и проинтегрируем его по 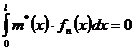 ,
,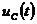 и
и 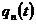 ;
;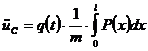 ;
;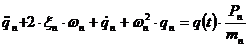 ,
,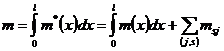 ;
;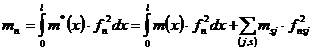 ;
;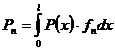 .
.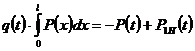 .
.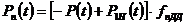 ,
,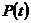 - отклонение силы двигателя;
- отклонение силы двигателя; 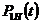 - отклонение силы давления жидкости перед входом в насос.
- отклонение силы давления жидкости перед входом в насос.