
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИЙСущность явления. Колебания механических систем могут вызываться не только внешними силами, непосредственно совершающими работу на основных перемещениях системы, но и внешними воздействиями, изменяющими параметры системы (жесткость, массу). В некоторых случаях при периодически изменяющихся параметрах возникают нарастающие колебания системы, имеет место так называемый параметрический резонанс.
Так же как и при обычном резонансе, при параметрическом резонансе колебания развиваются в связи с непрерывным поступлением энергии в систему Проследим Пусть стержень (рис. 7.1) совершает собственные поперечные колебания с частотой
При этом верхний шарнир получает небольшие вертикальные перемещения 
В данном случае жесткость стержня
где Таким образом, уравнение (7.1) может быть записано в виде
Если Сосредоточим внимание на одном периоде
Очевидно, что построить такие решения можно всегда, хотя бы путем численного интегрирования уравнения (7.2). Тогда общее решение уравнения (7.2) получит вид где Вычислим значения
Если предположить, что выполняются равенства
где
т. е. к квадратному уравнению относительно Свободный член уравнения (7.7) тождественно равен единице. В самом деле,
Умножая первое из этих равенств на
т.е.
Таким образом, характеристический множитель определяется равенством
где
Очевидно, что если то одно из значений Пограничным является случай Вычисление решений Практически более важен случай, когда параметр меняется по гармоническому закону
При этом уравнение (7.1) получает вид Это уравнение, называемое уравнением Матье, хорошо изучено. Характер его решений зависит от двух безразмерных коэффициентов. В самом деле, введя «безразмерное» время где
Коэффициенты l (характеризующий отношение собственной частоты системы при среднем значении параметра Такая диаграмма (диаграмма Айнса-Стретта) представлена на рис. 7.3. Области устойчивости на рисунке заштрихованы. Таким образом, для того чтобы определить, устойчиво или неустойчиво движение, описываемое уравнением (7.9), достаточно вычислить коэффициенты l, q, нанести соответствующую точку на диаграмму и установить, попадает ли она в устойчивую (заштрихованную) или в неустойчивую (белую) область. Проследим, как изменяется устойчивость системы при изменении частоты |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 594. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
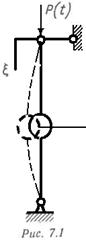 Примером параметрических колебаний является раскачивание на качелях. В этом случае удается увеличивать размахи колебаний только за счет периодического изменения расстояния центра тяжести системы от точки подвеса качелей. Тот же процесс может быть воспроизведен на маятнике с переменной длиной. Примером параметрического возбуждения колебаний является также явление динамической неустойчивости стержней (рис. 7.1), когда под действием периодически изменяющейся продольной силы стержень совершает поперечные колебания.
Примером параметрических колебаний является раскачивание на качелях. В этом случае удается увеличивать размахи колебаний только за счет периодического изменения расстояния центра тяжести системы от точки подвеса качелей. Тот же процесс может быть воспроизведен на маятнике с переменной длиной. Примером параметрического возбуждения колебаний является также явление динамической неустойчивости стержней (рис. 7.1), когда под действием периодически изменяющейся продольной силы стержень совершает поперечные колебания.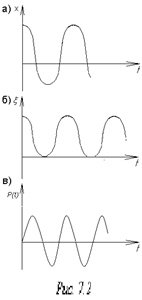 этот процесс на примере динамической неустойчивости стержня.
этот процесс на примере динамической неустойчивости стержня.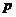 (рис. 7.2,а):
(рис. 7.2,а):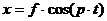
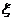 с удвоенной частотой (рис. 7.2,б). Он опускается вниз при отклонениях груза
с удвоенной частотой (рис. 7.2,б). Он опускается вниз при отклонениях груза 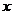 влево и вправо и занимает наивысшее положение, когда груз проходит положение статического равновесия. Если продольная сила изменяется также с частотой вдвое большей, чем частота поперечных колебаний груза (рис. 7.2, в), то она при каждом цикле совершает работу и энергия системы непрерывно нарастает. Составим уравнение движения груза
влево и вправо и занимает наивысшее положение, когда груз проходит положение статического равновесия. Если продольная сила изменяется также с частотой вдвое большей, чем частота поперечных колебаний груза (рис. 7.2, в), то она при каждом цикле совершает работу и энергия системы непрерывно нарастает. Составим уравнение движения груза 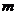 , закрепленного на стержне:
, закрепленного на стержне: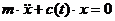 (7.1)
(7.1)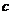 является функцией времени, так как она зависит от величины продольной силы
является функцией времени, так как она зависит от величины продольной силы 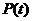 , приложенной в данный момент. В соответствии с приближенной формулой
, приложенной в данный момент. В соответствии с приближенной формулой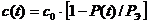 ,
,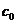 - жесткость стержня при отсутствии продольной силы;
- жесткость стержня при отсутствии продольной силы; 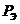 эйлерова критическая сила для стержня.
эйлерова критическая сила для стержня.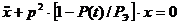
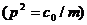 (7.2)
(7.2)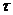 ) функцией времени, то уравнение (7.2) называется уравнением Хилла.
) функцией времени, то уравнение (7.2) называется уравнением Хилла.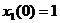 ,
, 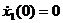 , (7.3)
, (7.3)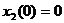 ,
, 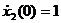 .
.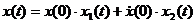 , (7.4)
, (7.4)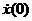 и
и 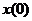 — начальные значения скорости и смещения.
— начальные значения скорости и смещения. в конце периода при
в конце периода при 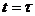 :
: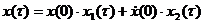 , (7.5)
, (7.5)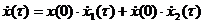 .
.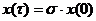 ,
, 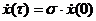 , (7.6)
, (7.6)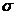 — число, большее единицы, то это означает, что в течение периода
— число, большее единицы, то это означает, что в течение периода 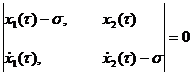 ,
,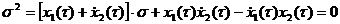 . (7.7)
. (7.7)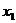 и
и 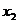 являются решениями уравнения (7.1):
являются решениями уравнения (7.1):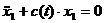 ,
, 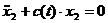 .
.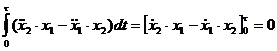 ,
,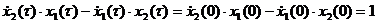 ,
,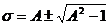 ,
,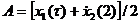 .
.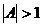 , (7.8)
, (7.8)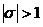 и движение неустойчиво. Если
и движение неустойчиво. Если 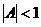 , то действительные значения
, то действительные значения 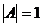 ,
, 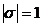 . Таким образом, для того чтобы установить, имеет ли место параметрический резонанс при данном законе изменения параметра, необходимо вычислить решения
. Таким образом, для того чтобы установить, имеет ли место параметрический резонанс при данном законе изменения параметра, необходимо вычислить решения 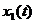 ,
, 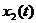 и проверить соблюдение неравенства (7.8).
и проверить соблюдение неравенства (7.8).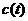 меняется по кусочно-постоянному закону (например, если в течение половины периода продольная сила постоянная сжимающая, а в течение второй половины — постоянная растягивающая).
меняется по кусочно-постоянному закону (например, если в течение половины периода продольная сила постоянная сжимающая, а в течение второй половины — постоянная растягивающая).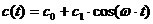 .
.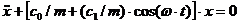 . (7.9)
. (7.9)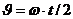 , приведем уравнение (7.9) к виду
, приведем уравнение (7.9) к виду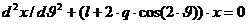 , (7.10)
, (7.10)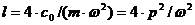 ,
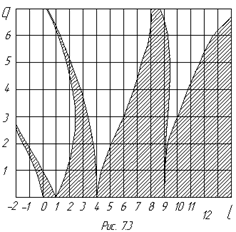
, 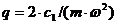 .
.
 к частоте изменения параметра) и q (характеризующий степень изменения параметра) полностью определяют устойчивость движения. Плоскость изменения l и q может быть разделена на области, соответствующие устойчивым и неустойчивым движениям.
к частоте изменения параметра) и q (характеризующий степень изменения параметра) полностью определяют устойчивость движения. Плоскость изменения l и q может быть разделена на области, соответствующие устойчивым и неустойчивым движениям. . В этом случае отношение q/l сохраняет постоянное значение и соответствующая точка на диаграмме Айнса-Стретта движется по лучу, проходящему через начало координат. При этом точка последовательно попадает то в области устойчивости, то в области неустойчивости. Как легко видеть, при малом изменении параметра (q мало) неустойчивость имеет место при значениях параметра /=1,4, 9, ..., т. е. при отношениях
. В этом случае отношение q/l сохраняет постоянное значение и соответствующая точка на диаграмме Айнса-Стретта движется по лучу, проходящему через начало координат. При этом точка последовательно попадает то в области устойчивости, то в области неустойчивости. Как легко видеть, при малом изменении параметра (q мало) неустойчивость имеет место при значениях параметра /=1,4, 9, ..., т. е. при отношениях 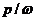 = 1/2; 1; 3/2; 2; 5/2 и т. д.
= 1/2; 1; 3/2; 2; 5/2 и т. д.