
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Отметим свойства вынужденных колебаний, вытекающие из уравнения
- Вынужденные колебания происходят с частотой возмущающей силы. - Вынужденные колебания в отличие от свободных ни в чем не зависят от начальных условий. Поэтому для изменения, например, амплитуды вынужденных колебаний необходимы (при заданной возмущающей силе) существенные изменения параметров системы: ее жесткости, распределения масс, тогда как в свободных колебаниях для этого достаточно изменения начального отклонения или начальной скорости. - Если k > p, то знак отклонения q3, будет совпадать со знаком силы Q, т. е. сила и вызванные ею вынужденные перемещения будут находиться в одной фазе. Если k < p, то знак силы будет противоположен знаку отклонения. Переписав для этого случая уравнение (1.6) следующим образом:
-
которую можно раскрыть по правилу Лопиталя, заменив дробь в квадратных скобках пределом при p
Таким образом, общий интеграл (1.5) будет иметь вид
И здесь, как в (1.5), движение осциллятора представляет линейное наложение трех колебательных движений, но с одним существенным отличием от (1.5): вынужденные колебания представлены в нем непериодическим членом
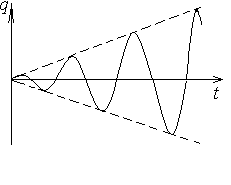
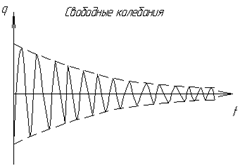
в коэффициент которого входит множителем время t. Такой член называется вековым. С течением времени он растет по абсолютной величине безгранично, причем определяемые им колебания происходят с возрастающими по линейному закону отклонениями, как показано на рисунке. Совпадение частоты возмущающей силы с собственной частотой системы и сопровождающие его явления носят название резонанса.  При наличии сопротивления, которое мы, как и раньше, примем пропорциональным первой степени скорости
мы найдем только одно решение, годное для любых значений p, в частности, и для резонансного p = k. В самом деле, уравнение колебаний линейного осциллятора в прежних обозначениях будет в этом случае иметь вид
Его общее решение найдется как сумма общего решения уравнения без правой части:
и частного решения уравнения (1.7) с правой частью. Решения уравнения (1.8) при различных соотношениях между n и k нам известны. В частности, при n < кk решение этого уравнения
определяет свободные затухающие колебания. Частное решение q2 уравнения (1.7) мы будем искать, положив
и подбирая величины A и
получающихся при сравнении коэффициентов при
Общийинтеграл уравнения (1.7), таким образом, имеет вид
Если
На рисунке представлен общий ход установления колебательного режима системы с сопротивлением при действии на нее гармонической возмущающей силы. Из уравнения (1.10) можно сделать несколько выводов. Вынужденные колебания и при наличии сопротивлений происходят с частотой возмущающей силы. Это всеобщий закон вынужденных колебаний линейного осциллятора, имеющий место независимо от условий, в каких происходят его вынужденные колебания, в частности, независимо от того, имеются ли в системе сопротивления или нет. Амплитуда вынужденных колебаний от начальных условий и времени не зависит. С течением времени она не изменяется и, следовательно, вынужденные колебания, в отличие от свободных, от сопротивлений не затухают. При резонансе, когда p = k, амплитуда вынужденных колебаний остается конечной и притом не самой большой из возможных ее значений для данной системы. В самом деле, разыскивая значение p, при котором амплитуда
(1.11) достигает максимума, найдем, что это случится, когда
т.е. до наступления резонанса, при p < k В вынужденных колебаниях с сопротивлением всегда имеет место сдвиг фазы колебания по сравнению с фазой возмущающей силы. Величина
Максимальное значение, равное Амплитудой вынужденных колебаний определяются максимальные динамические напряжения, возникающие в упругих системах от воздействия на них гармонических возмущающих сил. В высшей степени важно заметить, что величина этих напряжений, как и амплитуды А, зависит не столько от величины возмущающей силы, сколько от частоты ее изменений во времени. При одном и том же значении Н амплитуда и возникающие в системе напряжения могут значительно изменяться в зависимости от изменений частоты р. Для оценки этих изменений их сравнивают со статическим отклонением А0 системы при действии на нее силы Н
Отношение амплитуды А к А0, равное
где a=p/к, b=n/k, называется коэффициентом динамичности. Коэффициент динамичности показывает, во сколько раз максимальное динамическое отклонение при вынужденных колебаниях от силы
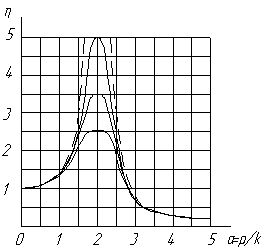
Эта кривая имеет разрыв в точке а = 1. Из рассмотрения резонансных кривых (рис.) обнаруживается следующий факт, имеющий значение в приближенных расчетах амплитуд вынужденных колебаний. В областях, достаточно далеких от резонанса, амплитуды при относительно малом сопротивлении почти не отличаются от соответствующих амплитуд вынужденных колебаний без сопротивления, определяемых более простой формулой
В этих областях при вычислении амплитуд можно совсем не учитывать сопротивлений, которые вообще с трудом поддаются точному определению. Хотя амплитуды вынужденных колебаний с сопротивлением остаются конечными и при резонансе, однако при более или менее продолжительной работе деталей машин в резонансных условиях всегда имеется опасность полного или частичного их разрушения от усталостных напряжений. При проектировании конструкции, подверженной воздействиям возмущающих сил, стараются, поэтому подобрать соотношения размеров и прочности ее деталей так, чтобы по возможности отодвинуть условия нормального режима работы ее от резонансных условий. Для той же цели служат специальные устройства, как, например, нелинейные муфты, виброгасители и т. п.
Автоколебания.
Колебания системы, определяемые изменением только одной нормальной координаты, называются главными колебаниями. Система с n степенями свободы в общем случае может совершать n независимых гармонических главных колебаний, каждому из которых соответствует определенное значение частоты pk. В обычных условиях при колебаниях системы изменяются все ее нормальные координаты. Малые колебания системы с n степенями свободы около положения устойчивого равновесия, определяемые изменениями обобщенных координат, представляют собой линейное наложение n главных гармонических колебаний. В этом разложении колебательного процесса, совершаемого системой, на ряд простых гармонических колебаний и заключается, в применении к нашей задаче, физический смысл приведения кинетической и потенциальной энергии к нормальным координатам. Главные колебания системы чаще называют собственными колебаниями, а их частоты – собственными частотам системы. Система с n степенями свободы имеет n, в общем случае различных, собственных частот.
АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ.
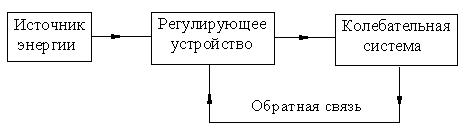
Автоколебания — один из самых распространенных видов свободных нелинейных колебаний неконсервативных систем. Часто ими пользуются для создания автоматически действующих незатухающих колебательных систем, как, например, в часах, поршневых двигателях, музыкальных духовых язычковых и смычковых струнных инструментах. Еще чаще автоколебания, возникающие во многих аппаратах и механизмах, оказываются вредными для нормальной работы, а иногда даже и целости последних. Таковы, например, автоколебания в системах автоматического регулирования. Последние уже по самому устройству своему сходны с автоколебательными системами, так что почти всегда при конструировании регуляторов приходится принимать специальные меры к устранению условий, при которых возможно возникновение автоколебаний. Весьма опасными являются автоколебания крыльев и хвостового оперения самолета — флаттер, — возникающие при определенных скоростях полета и приводящие иногда к полному разрушению самолета и его гибели. Много примеров автоколебательных систем приведено в прекрасной книге А. А. Харкевича «Автоколебания» [53], чтение которой может служить введением в общую теорию автоколебаний. Автоколебательные системы относятся к системам неконсервативным, так как в составе действующих на такие системы сил имеются сопротивления, и движение системы сопровождается расходом энергии. В этом отношении автоколебательные системы ведут себя аналогично диссипативным. Но в то время как в диссипативных системах энергия, расходуемая на преодоление сопротивлений, ничем не компенсируется и колебания таких систем затухают, в автоколебательных системах расход энергии на сопротивление точно компенсируется поступлениями из некоторого входящего в состав системы неколебательного источника — поступлениями, дозировка которых по времени подачи и по величине регулируется самой колебательной системой. Вследствие этого в автоколебательной системе могут возникать устойчивые периодические незатухающие колебания — автоколебания. Примером таких колебаний могут служить колебания маятника часов, в которых энергия падающего груза передается через храповой механизм маятнику порциями, величина и время подачи которых определяются колебаниями самого маятника. Способ компенсации расхода энергии является наиболее характерным свойством автоколебательной системы, по которому большей частью и распознаются эти системы в отличие от систем диссипативных, или систем, совершающих вынужденные колебания под действием периодических возмущающих сил. Таким же характерным свойством автоколебательной системы является наличие в ее конструктивной схеме следующих четырех частей: - постоянный (неколебательный) источник энергии; - колебательная система; - устройство, регулирующее поступления в колебательную систему энергии из источника энергии; - обратная связь между колебательной системой и регулирующим устройством, осуществляющая управление дозировкой подачи энергии в колебательную систему. Схема автоколебательной системы представлена на рисунке ниже. В автоколебательной системе регулирующее устройство управляет движением колебательной системы, а эта последняя через обратную связь управляет работой регулирующего устройства.
В этом двустороннем взаимодействии колебательной системы и регулирующего устройства с помощью обратной связи и осуществляется самоуправление энергетическим балансом системы, в результате чего в ней могут возникнуть устойчивые незатухающие колебания. Колебания эти, как правило, не зависят от начальных условий. В автоколебательных системах с самовозбуждением при любых начальных условиях система стремится к некоторому устойчивому периодическому движению. Принимая во внимание сделанные замечания, можно следующим образом определить автоколебательную систему, имея в виду главным образом ее конструктивную схему. Автоколебательной системой называется неконсервативная система, способная совершать незатухающие периодические колебания и характеризующаяся наличием следующих основных составных частей: 1) постоянного источника энергии; 2) колебательной системы: 3) устройства, регулирующего поступления энергии в колебательную систему из источника энергии; 4) обратной связи между колебательной системой и регулирующим устройством. Не всегда, однако, можно легко распознать автоколебательную систему по наличию в ней указанных частей. Механизм обратной связи иногда совсем не очевиден, так как во многих случаях обратная связь действует по скрытым путям, обнаружить которые не всегда удается. Автоколебательный характер некоторых простейших систем с одной степенью свободы может быть иногда обнаружен из рассмотрения уравнений движения системы. Существуют многочисленные критерии, позволяющие по некоторым свойствам коэффициентов дифференциального уравнения системы доказать возможность существования в этой системе незатухающих периодических колебаний. Ограничимся здесь формулировкой двух таких критериев — Льенара и Бендиксона, сделав предварительно следующее замечание. На фазовой плоскости периодические движения автоколебательной системы с одной степенью свободы изображаются замкнутыми траекториями, которые, по соображениям, приведенным дальше, называются предельными циклами. Критерий Льенара относится к системам, уравнение движения которых имеет вид
Уравнения весьма многих нелинейных систем могут быть приведены к такому виду, например уравнение
для которого А. Льенар дал описанный выше способ построения фазовых траекторий. В самом деле, продифференцировав это уравнение по t и положив
т. е. уравнение (1.1), в котором f(x) = F'(x) и g{x) = х. Сформулируем критерий Льенара. Система (1.1) будет иметь один устойчивый предельный цикл при следующих условиях, которым должны удовлетворять функции f(x) и g(x).
1. Функция f(x) должна быть четной, а g(x) — нечетной функцией переменной x. 2. f(x) < 0. 3. 4. 5. Функция f(x) имеет один нуль в точке x=a, a>0 и монотонно возрастает для Нечетность функции g(x) и условие xg{x) > 0 означают, что сила -g{x) всегда имеет знак, противоположный знаку x (знаку отклонения), т. е. действует как восстанавливающая сила в линейной упругой системе, всегда направленная к среднему, нулевому положению. Четность функции f(x) вместе с условием f(0) < 0 означает, что коэффициент сопротивления имеет отрицательный знак для малых значений Условия 4 и 5 выражают прежде всего, что система (1.1) не является диссипативной вблизи нулевого положения, чем подтверждают аналогичный вывод из условий 1 и 2. Кроме того, из этих условий следует, что рассматриваемая система представляет собой систему с самовозбуждением с графиком функции F(x), имеющим в точке x = 0 ниспадающую часть.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 500. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
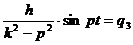
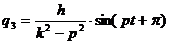
 Мы можем сказать, что при k < p возмущающая сила и вызванные ею колебания находятся в противоположных фазах. Когда k = p, выражение (1.6) теряет смысл. Теряет смысл также и слагаемое общего решения (1.5), соответствующее свободным сопровождающим колебаниям. Однако рассматриваемые совместно, оба названные слагаемые при k = p дают только неопределенность
Мы можем сказать, что при k < p возмущающая сила и вызванные ею колебания находятся в противоположных фазах. Когда k = p, выражение (1.6) теряет смысл. Теряет смысл также и слагаемое общего решения (1.5), соответствующее свободным сопровождающим колебаниям. Однако рассматриваемые совместно, оба названные слагаемые при k = p дают только неопределенность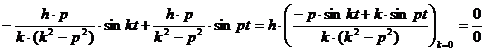
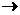 k отношения производных по p от числителя и знаменателя:
k отношения производных по p от числителя и знаменателя: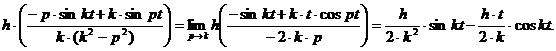
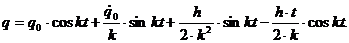
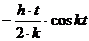
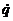 , положив
, положив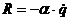 ,
,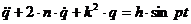 (1.7)
(1.7)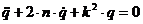 (1.8)
(1.8)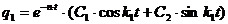 ,
, 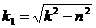
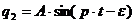
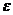 так, чтобы это выражение, будучи подставлено в уравнение (1.7), обратило его в тождество. Из уравнений
так, чтобы это выражение, будучи подставлено в уравнение (1.7), обратило его в тождество. Из уравнений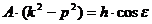
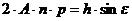
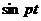 и
и 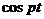 в обеих частях уравнения (1.7), находим
в обеих частях уравнения (1.7), находим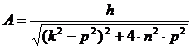 ,
, 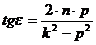 .
.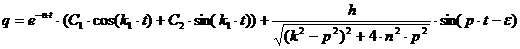
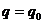 и
и 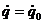 в начальный момент времени
в начальный момент времени 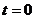 , то
, то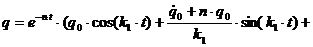
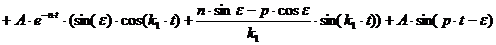 (1.9)
(1.9)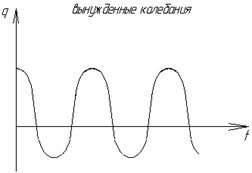
 Первые два слагаемых полученного решения соответствуют свободным и свободным сопровождающим колебаниям. И те, и другие с течением времени затухают, так что через более или менее продолжительный промежуток времени ими можно будет вообще пренебречь и считать, что в дальнейшем движении система совершает только чисто вынужденные колебания согласно уравнению
Первые два слагаемых полученного решения соответствуют свободным и свободным сопровождающим колебаниям. И те, и другие с течением времени затухают, так что через более или менее продолжительный промежуток времени ими можно будет вообще пренебречь и считать, что в дальнейшем движении система совершает только чисто вынужденные колебания согласно уравнению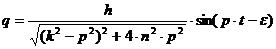 (1.10)
(1.10) Этим уравнением будет определяться установившийся колебательный режим линейного осциллятора и при других отношениях между n и k: когда n > k или n = k.
Этим уравнением будет определяться установившийся колебательный режим линейного осциллятора и при других отношениях между n и k: когда n > k или n = k.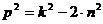 ,
,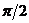 , сдвиг фазы имеет при резонансе, когда p = k.
, сдвиг фазы имеет при резонансе, когда p = k.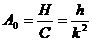
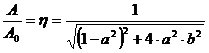
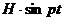 больше максимального статического отклонения от постоянной силы
больше максимального статического отклонения от постоянной силы  . На рисунке резонансными кривыми представлен ход изменения абсолютной величины коэффициента динамичности
. На рисунке резонансными кривыми представлен ход изменения абсолютной величины коэффициента динамичности 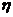 в зависимости от частоты возмущающей силы (от а = p/к) для некоторых значений коэффициента сопротивления b = n/к. Пунктиром показана резонансная кривая для n=0 в отсутствие сопротивления, когда коэффициент динамичности
в зависимости от частоты возмущающей силы (от а = p/к) для некоторых значений коэффициента сопротивления b = n/к. Пунктиром показана резонансная кривая для n=0 в отсутствие сопротивления, когда коэффициент динамичности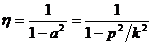
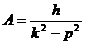
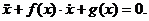 (1.1)
(1.1)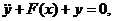
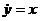 , получим
, получим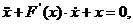
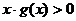 для всех
для всех 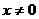 .
.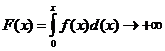 , когда
, когда 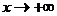 .
.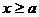 .
.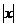 , т. е. при малых отклонениях сопротивление раскачивает систему. Для больших
, т. е. при малых отклонениях сопротивление раскачивает систему. Для больших