
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Что называется биномиальным распределением с параметрами n и p? Приведите пример опытов, в котором определена случайная величина, распределенная по биномиальному закону.Пусть производится определенное число п независимых опытов. В каждом из них с одной и той же вероятностью р может наступить некоторое событие А. Рассматриваемая случайная величина Х- число наступлений событий А в п опытах. Соответствующая таблица имеет вид:
где Pn(k)=Cnkpk(1-p)n-k
48. Какой закон распределения называется законом Пуассона? Увяжите с предельной теоремой Пуассона. Если число испытаний велико, а вероятность p появления события в каждом испытании очень мала, то используют следующую формулу
49. Как определяется независимость случайных величин? Игральную кость бросают 200 раз. Пусть X1 – число выпадений грани 1; X2 – число выпадений грани 2 . Будут ли зависимыми случайные величины X1 и X2 ? Ответ обоснуйте.
X и Y независимы, если выполняется равенство P(X=a, Y=b) = P(X=a)P(Y=b). P(X1=200) = (1/6)200 (т.к. опыт проводился 200 раз). Следовательно, можно записать P(X1=200, Y1=200) = 0. Однако такого быть не может, т.к. если одна грань выпала 200 раз, то вторая уже не может (она эти 200 раз НЕ ВЫПАЛА). Следовательно эти величины зависимы.
50. Пусть X,Y,X – независ СВ, принимающие с вероятностью 1\2 значения 0 и 1. Верно ли, что X+Y и Y+Z – независ СВ?
 1\8¹1\16 - зависимые.
Дайте определение математического ожидания дискретной случайной величины. Поясните его смысл на примере случайной величины с двумя возможными значениями, исходя из статистического определения вероятности
Пусть случайная величина X связана с некоторым опытом. Провели n испытаний и при этом возникла статистика
Найдем среднее значение X =
Lim X = X1*p1 + X2*p2 M(X)) Перечислите основные свойства математического ожидания дискретной случайной величины. Объясните, что понимается под суммой и произведением случайных величин. Математическим ожиданием дискретной случайной величины
Называется число Математическое ожидание имеет следующие свойства: 1) Математическое ожидание случайной величины равно ей самой: М(С)=С 2) .Постоянный множитель можно вынести за знак математического ожидания: М(сХ)=сМ(Х). Следовательно: M(aX+bY)=aM(X)+bM(Y) 3) Математическое ожидание суммы случайных величин равно сумме их мат. Ожиданий: 4) Если случайные величины 5) Мат. ожидание от функции Для определения суммы и произведения случ. вел. Х и У будем считать, что мы рассматриваем случайную величину
Приведите (с обоснованием) пример дискретного распределения вероятностей, для которого не существует математическое ожидание.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 731. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
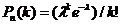 , где
, где 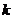 - число появлений события в n независимых испытаниях, l= np (среднее число появлений события в n испытаниях), и говорят, что с.в.распределена по закону Пуассона. (Есть спец.таблицы для нахождения P
- число появлений события в n независимых испытаниях, l= np (среднее число появлений события в n испытаниях), и говорят, что с.в.распределена по закону Пуассона. (Есть спец.таблицы для нахождения P 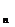 (k), зная
(k), зная 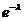

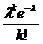

 è при n стремящимся к бесконечности = X1*p1 + X2*p2 т.к по статистическому определению вероятность события примерно равна отношению числа успехов к общему числу испытаний.
è при n стремящимся к бесконечности = X1*p1 + X2*p2 т.к по статистическому определению вероятность события примерно равна отношению числа успехов к общему числу испытаний. 
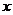 с законом распределения
с законом распределения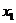



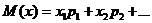
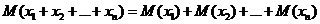
 независимы, то мат. ожидание их произведений равно произведению их мат. ожиданий:
независимы, то мат. ожидание их произведений равно произведению их мат. ожиданий: 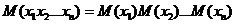
 равно:
равно: 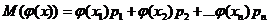
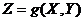 , где g(X,Y) – некоторая числовая функция. Тогда система (Х,У) характеризуется следующей таблицей:
, где g(X,Y) – некоторая числовая функция. Тогда система (Х,У) характеризуется следующей таблицей:


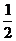
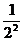
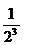
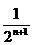
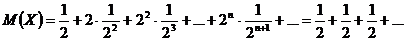 ряд расходится т.к. => нет математич. ожидания.
ряд расходится т.к. => нет математич. ожидания. 