Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Запишите приближённые формулы Пуассона. При каких условиях они дают хорошее приближение? Приведите примеры их применения.формулы Пуассона:
Что такое сл.величина? Дискретная величина? Что назыв функцией распределения случ. величины? Привести пример функции распределения некоторой дискретной сл вел и построить график. Величина, принимающая в результате испытания определенное значение, называется случайной величиной. Случайная величина Х называется дискретной, если множество ее возможных значений конечно или счетно: Х(Ω)={x1, x2,…} Функция, определенная в каждой точке х числовой оси формулой Fx(x)=F(x)=P(X<x) Называется функцией распределения случайной величины Х. Пример: Дан ряд распределения с.в. Х:
Найти и изобразить графически ее функцию распределения.
при х≤1, 0,4 при 1<х≤4, F(x)= 0,5 при 4<х≤5, 0,8 при 5<х≤7, 1,0 при х>7.
Сформулируйте основные свойства функции распределения сл величины и продемонстрируйте их на примере.
Пример!!!Р(Х=6)=F96+0)-F(6)=P(X<6+0)-P(X<6)=1-5/6=1/6 Может ли график функции распределения быть прямой линией? Ответ обоснуйте. Нет, не может, т.к.
Что такое дискретная случайная величина? Может ли таблица
Рассматриваться как закон распределения дискретной случайной величины?  СВ Х называется дискретной, если мн-во ее значений не более чем счетно, т.е конечно или счетно. По опр сумма значений строчке * должна быть равна 1. То есть, нет не может.
Дана дискретная случайная величина с законом распределения
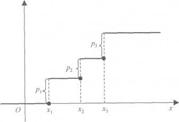
Что является её функцией распределения F(x)? Постройте график F(x) и опишите его точки разрыва. Как вычисляется вероятность Пусть хо - любое число. Среди чисел х1 , x2, ... выделим те, которые меньше х0. Пусть ими будут хi1, xi2 ,.... Событие x<х0 является суммой событий X = хi2, X – xi1 , ..., поэтому его вероятность равна pi1 + pi2 +... F(x)= ∑pi График для X на три значения: хь х2, хз. x1 < х2 < хз. График представляет собой ступенчатую ломаную со скачками в точках х1 х2, х3. Величины скачков равны соответственно p1,p2,p3 - Левее график совпадает с осью Ох, правее c прямой y=1. P(a≤X≤b)=P(b)-P(a).
46. Что называется геометрическим распределением с параметром p? Приведите пример опытов, в котором определена случайная величина, распределенная по геометрическому закону с параметром p? Производится ряд независимых опытов, в каждом из которых с одной и той же вероятностью наступает событие А. Опыты продолжаются до первого появления события А, после чего прекращаются. Рассматривается случайная величина - х число произведенных опытов. Составить для нее закон распределения. Возможные значения величины
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 549. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
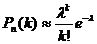 и
и 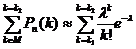 . Они дают хорошее приближение при больших n и малых p (npq£10). Пример: в тесто засыпают большое количество изюма (например, 10000 изюмин) и нужно оценить вероятность того, что в случайно выбранной булке, испечённой из этого теста, окажется, к примеру, ровно 2 изюмины). То есть получается, что p=2/10000 = 0,0002). В этом случае также npq<10. В итоге, можем применять приближённую формулу Пуассона.
. Они дают хорошее приближение при больших n и малых p (npq£10). Пример: в тесто засыпают большое количество изюма (например, 10000 изюмин) и нужно оценить вероятность того, что в случайно выбранной булке, испечённой из этого теста, окажется, к примеру, ровно 2 изюмины). То есть получается, что p=2/10000 = 0,0002). В этом случае также npq<10. В итоге, можем применять приближённую формулу Пуассона.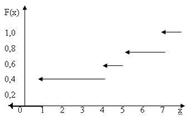
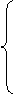 0
0
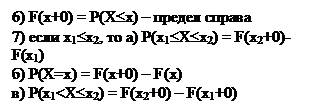
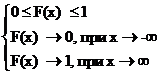
 ?
?