
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
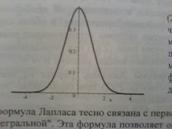
Может ли наиболее вероятное число успехов в схеме Бернулли отличаться от математического ожидания числа успехов на 2? Ответ обоснуйте.По схеме Бернулли наиболее вероятное число успехов: k=np+p. Мат. ожидания: так как схему Бернулли можно представить как биноминальное распределение M(x)=np np+p-np=p Следовательно, в схеме Бернулли наиболее вероятное число успехов может отличаться от мат. ожидания на число р - вероятность успеха и известно, что p+q=1, p=1-q p<1. А значит отличаться на 2 не может. 35. Запишите локальную приближенную формулу Лапласа, приведите основные свойства функции Гаусса ϕ (x) и укажите ее график. При каких условиях данная формула дает хорошее приближение? Какие условия применимости отличают эту формулу от приближенной формулы Пуассона? Если число опытов достаточно велико но не бесконечно, а вероятность появления события А в каждом опыте не стремится к 0, применяют локальную и интегральную теоремы Лапласа Локальная теорема Лапласа.Вероятность того, что в n независимых испытаниях в каждом из которых вероятность появления события А равно р причем 1>р>0, то это событие наступает ровно m раз приблизительно равна
36. Запишите интегральную приближенную формулу Лапласа и приведите основные свойства функции Лапласа Φ(x) . При каких условиях данная формула дает хорошее приближение? Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях в каждом из которых вероятность появления события А равно р, причем 1>р>0, то событие А наступит не менее m1 раз и не более m2 раза приблизительно равно
Эта формула дает хорошее приближение при больших n 37. Укажите выражение для функции Лапласа Ф(x). Докажите нечётность функции Ф(x) и нарисуйте график y=Ф(x). Чему равно Ф(12)? Функция: Ф(x) =  Доказ-во Ф(-x) = -Ф(x): запишем выражение Ф(-x) = График: симметричен относительно начала координат, проходит через (0;0). Горизонтальные асимптоты: -0,5 и 0,5. Ф(-12) = -0,5.
Используя интегральную приближённую формулу Лапласа, выведите формулу для оценки отклонения относительной частоты события А от вероятности p наступления A в одном опыте. В условиях схемы Бернулли с заданными значениями n и p для данного e>0 оценим вероятность события
Сформулируйте и докажите предельную теорему Пуассона. При n®¥, p®0 b, а величина l = np остаётся постоянной Док-во: имеем:
|
||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 533. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
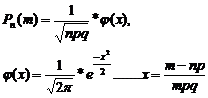
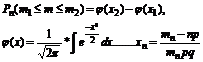
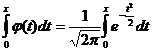
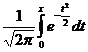 и выполним замену z = -t, dz = -dt, при этом нижний предел интегрирования не изменится, а верхний станет равным x. Таким образом, Ф(-x) =
и выполним замену z = -t, dz = -dt, при этом нижний предел интегрирования не изменится, а верхний станет равным x. Таким образом, Ф(-x) = 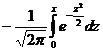 = -Ф(x), ч.т.д.
= -Ф(x), ч.т.д.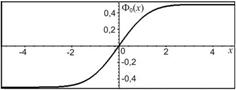
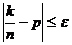 , где k – число успехов в n опытах. Это неравенство эквивалентно |k-np|£en, т.е. -en £ k-np £ en или np-en £ k £ np+en. Таким образом, речь идёт о получении оценки для вероятности события k1 £ k £ k2, где k1 = np-en, k2 = np+en. Применяя интегральную приближённую формулу Лапласа, получим: P(
, где k – число успехов в n опытах. Это неравенство эквивалентно |k-np|£en, т.е. -en £ k-np £ en или np-en £ k £ np+en. Таким образом, речь идёт о получении оценки для вероятности события k1 £ k £ k2, где k1 = np-en, k2 = np+en. Применяя интегральную приближённую формулу Лапласа, получим: P( 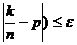 »
» 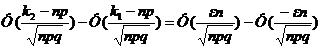 . С учётом нечётности функции Лапласа получаем приближённое равенство P(
. С учётом нечётности функции Лапласа получаем приближённое равенство P( 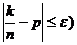 » 2Ф(
» 2Ф( 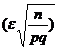 . Примечание: т.к. по условию n=1, то подставляем вместо n единицу и получаем окончательный ответ.
. Примечание: т.к. по условию n=1, то подставляем вместо n единицу и получаем окончательный ответ.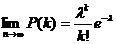 .
.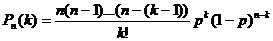 , и так как p=l/n, то
, и так как p=l/n, то 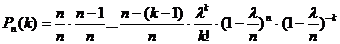 . Выражение
. Выражение 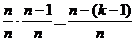 - это произведение k множителей, стремящихся к 1; поэтому и всё произведение стремится к 1. Выражение
- это произведение k множителей, стремящихся к 1; поэтому и всё произведение стремится к 1. Выражение 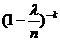 стремится к 1. Что касается выражения
стремится к 1. Что касается выражения 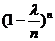 , то его можно записать в виде
, то его можно записать в виде 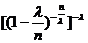 . Замечая, что выражение в квадратных скобках имеет пределом число
. Замечая, что выражение в квадратных скобках имеет пределом число 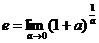 , получим окончательно:
, получим окончательно: 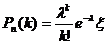 , где x®1. Отсюда тотчас же следует формула, указанная в теореме.
, где x®1. Отсюда тотчас же следует формула, указанная в теореме.