
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Выведите формулу для наиболее вероятного числа успехов в серии n испытаний по формуле Бернулли.По формуле Бернулли, событие «произошло 0 успехов в Чтобы выяснить это, сравним отношение
Видим, что (a)
(b)
(c)
Рассмотрим два случая: В первом случае пусть
Во втором случае пусть
Действительно, неравенство Видим, что в зависимости от того, является число Сформулируем уже доказанное утверждение в виде теоремы. Теорема 11. В a) единственное число б) два числа 33. Пусть Рассмотрим два соседних числа  Таким образом, для всех значений k меньших чем np-q< Если же Если число |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 604. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 испытаниях» имеет вероятность
испытаниях» имеет вероятность  , 1 успех — вероятность
, 1 успех — вероятность 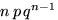 и т.д. Какое же число успехов наиболее вероятно? Иначе говоря, при каком
и т.д. Какое же число успехов наиболее вероятно? Иначе говоря, при каком 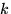 достигается максимум
достигается максимум  ?
? с единицей.
с единицей.
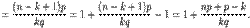
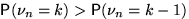 при
при  , то есть при
, то есть при  ;
; при
при  , то есть при
, то есть при  ;
; при
при 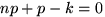 , что возможно лишь если
, что возможно лишь если  — целое число.
— целое число. и
и  .
. . Из полученных выше неравенств сразу следует, что
. Из полученных выше неравенств сразу следует, что
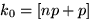 (целая часть числа
(целая часть числа  , например, следует из (b), примененного для
, например, следует из (b), примененного для  .
. , либо одно «наиболее вероятное» число успехов
, либо одно «наиболее вероятное» число успехов  наиболее вероятным числом успехов является
наиболее вероятным числом успехов является - вероятностьk успехов в серииnнезависимых испытаний с вероятностью успехаpв каждом испытании. При какомk вероятность
- вероятностьk успехов в серииnнезависимых испытаний с вероятностью успехаpв каждом испытании. При какомk вероятность  ?
? . Между ними имеет место одно из соотношений:
. Между ними имеет место одно из соотношений:  (меньше, равно или больше) или, что эквивалентно,
(меньше, равно или больше) или, что эквивалентно,  . Подставляя вместо числителя и знаменателя их выражения по формулам
. Подставляя вместо числителя и знаменателя их выражения по формулам  ,
,  или учитывая, что
или учитывая, что  , получим соотношения
, получим соотношения  или
или  . Собирая все слагаемые с множителем k и учитывая , что p+q=1 , получим эквивалентные соотношения
. Собирая все слагаемые с множителем k и учитывая , что p+q=1 , получим эквивалентные соотношения  . Обозначим число np+p через
. Обозначим число np+p через  . Тогда перепишется :
. Тогда перепишется :  .
. справедливо неравенство
справедливо неравенство  ,для
,для  ( это возможно только в том случае, когда
( это возможно только в том случае, когда 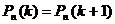 ,наконец, при
,наконец, при  выполняется неравенство
выполняется неравенство 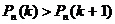 .Тем самым при значениях
.Тем самым при значениях  функция
функция  , которое заключено между
, которое заключено между 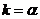 .
. не является целым, то наиболее вероятное число успехов равно ближайшему к
не является целым, то наиболее вероятное число успехов равно ближайшему к