
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Парабола. Определение. Вывод канонического уравнения.Парабола – множество точек плоскости, равноудалённых от некоторой точки, называемой фокусом параболы, и некоторой прямой, называемой директрисой параболы. Расстояние между фокусом и директрисой называется параметром параболы и обозначается через р>0. Пусть M(x;y) – произвольная точка M с F. Проведем отрезок MN перпендикулярно директрисе. Согласно определению, MF=MN.
Эллипс.
MF1+MF2=2a
Можно привести к виду : a2-c2= b2; можно ввести обозначения, т к по определению a>c. Найдём точки пересечен. эллипса с координатн. осями. Для этого полагаем: x=0, y=0, Величина b наз. малой полуосью эллипса, а- большой полуосью. Отношение с/a=E называется эксцентриситетом, т к с<0, E<1. В частности, когда полуоси эллипса равны a=b=R
x2+y2=R2 - частный случай эллипса. Гипербола Гиперболой наз-ся множество точек плоскости, разность расстояний от которых, взятая по модулю до 2 данных точек, называемых фокусами гиперболы, есть величина постоянная и меньшая, чем расстояние между фокусами.
y
F1(-C;0) F2(c;0)
После упрощения это уравнение принимает вид: Найдем точки пересечения гиперболы с координатными осями. Предположим:  y=o
Точки пересечения с осью Оу нет.
-а а
2 оси симметрии. Одна пересекает, другая нет. Ось симметрии, пересекающая гиперболу, наз-ся её действиетльной осью. В нашем случае, это ось Ох, ось Оу- мнимая ось. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 548. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 - каноническое ур-е параболы
- каноническое ур-е параболы Эллипсом называется множество точек плоскости, сумма расстояния от которых до 2-х данных точек, наз. фокусами эллипса, есть величина постоянная и большая, чем расстояние между фокусами.
Эллипсом называется множество точек плоскости, сумма расстояния от которых до 2-х данных точек, наз. фокусами эллипса, есть величина постоянная и большая, чем расстояние между фокусами.
 , y=±b
, y=±b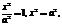 x=±a.
x=±a.
 M(x;y)
M(x;y)

 - каноническое уравнение гиперболы, где введено обозначение
- каноническое уравнение гиперболы, где введено обозначение  (c>a)
(c>a)

