
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейнонезависимые системы векторов.Векторы Векторы Заметим, что если хотя бы один из данных векторов не яв-ся нулевым, то эти векторы линейно зависимы. Теорема. Необходимым и достаточным условием линейной зависимости двух векторов яв-ся их коллинеарность. Док-во: 1. Докажем необходимость. Пусть векторы 2. Достаточность. Пусть
Среди двух неколлинеарных векторов не может быть нулевого вектора. Определение. 3 вектора наз-ся компланарными, если они лежат в одной плоскости либо в параллельных плоскостях. Теорема. Необходимым и достаточным условием линейной зависимости 3 векторов яв-ся их компланарность. Теорема. Любые 4 вектора в трехмерном пространстве линейно зависимы. Следствие. Каковы бы ни были 3 некомпланарных вектора 18. Векторы в трехмерном пространстве.
Вектор наз-ся нулевым, если его начало и конец совпадают.  Векторы наз-ся коллинеарными, если они лежат на одной прямой, либо на параллельных прямых. Два вектора наз-ся равными, если они коллинеарные, имеют одинаковую длину и одинаково направлены.
a≠b a≠b a=b Декартова прямоугольная система координат. В качестве базиса декартовой прямоуг. сист. координат выбирают 3 взаимно перпендикулярных вектора
Удобно пользоваться координатными осями. x, y, z – декартовы координаты вектора а. Координаты любой точки М пространства определяют как координаты вектора r, проведённого из начала координат в точку. Можно показать, что декартовы координаты вектора = его проекциям на координатные оси. Координаты точки декартовой системы координат = отрезкам, отсекаемым проекциями точки на координатных осях. Модуль вектора |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 534. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 наз-ся линейно зависимыми, если существуют числа
наз-ся линейно зависимыми, если существуют числа  среди которых хотя бы одно отлично от 0, то вып-ся равенство:
среди которых хотя бы одно отлично от 0, то вып-ся равенство:  (1).
(1). .
. линейно зависимы, то есть справедливо равенство
линейно зависимы, то есть справедливо равенство  , где хотя бы одно из чисел, например,
, где хотя бы одно из чисел, например,  ≠0. Тогда имеем:
≠0. Тогда имеем:  , откуда следует, что эти векторы коллинеарны.
, откуда следует, что эти векторы коллинеарны. коллинеарны, тогда, согласно теореме из предыдущего параграфа,
коллинеарны, тогда, согласно теореме из предыдущего параграфа,  .
. . Причем, коэффициент перед вектором а1 отличен от нуля. Тогда, согласно определению, эти векторы линейно зависимы. Очевидно, что если 2 вектора не коллинеарны , то они линейно независимые.
. Причем, коэффициент перед вектором а1 отличен от нуля. Тогда, согласно определению, эти векторы линейно зависимы. Очевидно, что если 2 вектора не коллинеарны , то они линейно независимые. , любой вектор
, любой вектор  пространства может быть представлен в виде αa+βb+γc=d, где α, β, γ – некоторые числа
пространства может быть представлен в виде αa+βb+γc=d, где α, β, γ – некоторые числа Вектором наз-ся направленный отрезок
Вектором наз-ся направленный отрезок  (Вектор приложен к точке А). Для обозначения длины вектора исп-ют символ І І (ІАВІ).
(Вектор приложен к точке А). Для обозначения длины вектора исп-ют символ І І (ІАВІ).

 , единичной длины
, единичной длины 


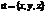 .
.
