
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Векторное произведение. Его свойства.
правая –-- левая. с=[a,b] – векторное произведение. Упорядоченная тройка некомпланарных векторов a, b, c с общим началом называется правой, если при наблюдении с конца вектора с кратчайший поворот от а к b осуществляется против часовой стрелки. Если орты декартовой системы координат I, j, k образуют правую тройку, то эта сист. координат называется правой, если левую – то левой. Векторным произведением двух векторов 1) |c|=|a|∙|b|∙sinj, где j - угол между векторами a и b. 2) вектор c^a и c^b (вектор с^плоскости, где лежат a и b). 3) векторы a, b, c образуют правую тройку.
Алгебраические свойства векторного произведения: 1) 2) 3) 4) Утверждение: необходимым и достаточным условием коллинеарности 2х векторов является равенство 0 их векторного произведения. Это следует из того, что sin0=0.
Выражение для векторного произведения в декартовых координатах. Пусть вектор
Более удобная для запоминания форма:
В справедливости последнего выражения можно убедиться, разлагая его по элементам первой строки.
Смешанное произведение трёх векторов. Его свойства и выражение в декартовых координатах. Смешанное произведение пусть векторы
Если бы векторы  Смешанное произведение 3х векторов Свойства смешанного произведения: 1) 2) смешанное произведение не изменяется при циклической перестановке векторов-сомножителей. 3) смешанное произведение изменяет свой знак на противоположный при перемене мест 2х рядом стоящих сомножителей. Необходимым и достаточным условием компланарности 3х векторов является равенство нулю их смешанного произведения. Выражение в декартовых координатах. Пусть вектора имеют следующие координаты:
Мы знаем, что векторное произведение имеет следующие координаты:
В справедливости последнего выражения можно убедиться, разлагая определитель по элементам 3-й строки. Из вышесказанного следует, что условием компланарности 3х векторов является равенство нулю определителя, составленного из их декартовых координат.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 506. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 называется вектор
называется вектор  , обладающий следующими свойствами:
, обладающий следующими свойствами: Модуль векторного произведения = площади параллелограмма, построенного на этих векторах.
Модуль векторного произведения = площади параллелограмма, построенного на этих векторах.


 , т. к. sin0=0
, т. к. sin0=0 ,
,  , тогда векторное произведение равно:
, тогда векторное произведение равно:





 . Геометрический смысл:
. Геометрический смысл: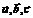 некомпланарны, проведём эти векторы из одной точки, построим на них параллелепипед, найдём его объём. Векторы
некомпланарны, проведём эти векторы из одной точки, построим на них параллелепипед, найдём его объём. Векторы 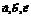 образуют правую тройку.
образуют правую тройку. V=Sосн∙Н
V=Sосн∙Н 


 .
.
 образовали левую тройку, то мы получили бы
образовали левую тройку, то мы получили бы  ,
, 
 правая и отрицательно, если эта тройка левая.
правая и отрицательно, если эта тройка левая.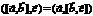 - в смешанном произведении можно менять порядок скалярного и векторного произведения. Это можно проследить из геометрического смысла выражений.
- в смешанном произведении можно менять порядок скалярного и векторного произведения. Это можно проследить из геометрического смысла выражений. . Это свойство вытекает из того, что векторное произведение изменяет свой знак при перемене мест сомножителей.
. Это свойство вытекает из того, что векторное произведение изменяет свой знак при перемене мест сомножителей. 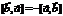

 ,
,  ,
, 
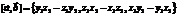 . Пусть
. Пусть  . По определению смешанного произведения,
. По определению смешанного произведения,  , следовательно,
, следовательно, 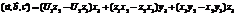 . Для запоминания более удобно следующее выражение:
. Для запоминания более удобно следующее выражение: