Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Общее уравнение плоскости и прямой на плоскости.Положение плоскости в пространстве полностью определяется некоторой точкой, принадлежащей плоскости, и направлением вектора, перпендикулярного плоскости.
Пусть М – произвольная точка плоскости, тогда вектор Проведём в М0 и М из начала координат Уравнение плоскости, заданное принадлежащей ей точкой, определяемой радиус-вектором Пусть М0(x0,y0,z0), M(x,y,z), тогда вектор Пусть вектор A(x-x0)+B(y-y0)+C(z-z0)=0. (2) Это уравнение плоскости, проходящей через точку (x0,y0,z0) ^-но вектору {A,B,C} в координатной плоскости. Аналогично можно получить уравнение прямой на плоскости, заданной точкой М0(x0,y0) и вектором N{A,B}. Рассуждая аналогично, можно сказать, что радиус-вектор, проведённый из начала координат в произвольную точку прямой будет удовлетворять уравнению прямой на плоскости в векторной форме. Рассуждая аналогично, можно получить: A(x-x0)+B(y-y0)=0. (4) Преобразуем уравнение (2) Ax+By+Cz-(Ax0+By0+Cz0)=0 Ax+By+Cz+D=0 (5) D= -(Ax0+By0+Cz0) Уравнение D – это общее уравнение. Можно показать, что уравнение любой плоскости в пространстве может быть представлено в виде (5). Любое уравнение вида (5) – линейное относительно координат x y z, определяет некоторую плоскость в пространстве; преобразуя аналогично уравнение (4) получим Ах+Ву+С=0. (6) С= -(Ax0+By0) Уравнение (6) – общее уравнение прямой на плоскости. Можно показать, что уравнение любой прямой может быть представлено в виде (6) и что любое уравнение вида (6) линейное относительно координат х у и определяет некоторую прямую на плоскости.  Уравнение плоскости и прямой на плоскости в отрезках. Пусть некоторая плоскость не II ни одной из плоскостей декартовой системы координат
Такая плоскость отсекает на координатных осях отрезки, которые обозначим a, b и c. А(а,0,0), В(0,b,0), C(0,0,c). Уравнение этой плоскости может быть представлено в виде Ax+By+Cz+D=0. Потребуем, чтобы А(а,0,0) удовлетворяло этому уравнению. Подставляем координаты этой точки в уравнение (1) вместо x y z: A∙а+B∙0+C∙0+D=0 А= -D/а Аналогично из требования, чтобы В(0,b,0) удовлетворяла уравнению (1) имеем: A∙0+B∙b+C∙0+D=0, В=-D/ b. Точно так же подставляем в уравнение (1) координаты C(0,0,c). Находим: С= -D/с. Подставляя найденные значения коэффициентов А, В, С в уравнение (1), имеем Аналогично можно найти уравнение прямой на плоскости, отсекающей на координатных осях Ох и Оу соответственно отрезки a и b.
Потребуем, чтобы точки пересечения с осями удовлетворяли условию Ax+By+C=0
Преобразуем уравнение (2)
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 511. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 М0 – зафиксированная точка плоскости,
М0 – зафиксированная точка плоскости, 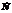 - вектор, ^-ный плоскости.
- вектор, ^-ный плоскости. ^
^  , т. е. скалярное произведение (
, т. е. скалярное произведение (  )=0
)=0 , тогда
, тогда  .
.  (1)
(1) и вектором
и вектором  - радиус-вектор, проведённый в произвольную точку плоскости – уравнение в векторной форме.
- радиус-вектор, проведённый в произвольную точку плоскости – уравнение в векторной форме. ,
, 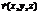 .
.  = r-r0={x-x0,y-y0,z-z0}
= r-r0={x-x0,y-y0,z-z0} , тогда уравненіе (1) можно переписать так:
, тогда уравненіе (1) можно переписать так:
 . Умножим обе части уравнения на
. Умножим обе части уравнения на  ; получаем:
; получаем:  - уравнение плоскости в отрезках.
- уравнение плоскости в отрезках.