
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные теоремы о пределахВ следующих теоремах мы не будем указывать, к чему → х, предполагая, что либо х→а либо х→∞. Т-ма1: Предел алгебраич. суммы конечного числа ф-ций = алгеб. сумме их пределов: lim (f1(x) + f2(x) + … + fn(x)) = lim f1(x) + lim f2(x) + … + lim fn(x); Т-ма 2. Предел произведения конечного числа ф-ций = произведению их пределов: lim (f1(x) * f2(x) * … *fn(x)) = lim f1(x) * lim f2(x) *… * lim fn(x); Постоянный множитель можно выносить за знак предела: lim C f(x)= C limf(x); C=const. Предел частного 2-х ф-ций = частному их пределов, если предел знаменателя отличен от 0:
Если для 2-х ф-ций выпол-ся нера-во f(x)>g(x), то для их пределов справедливо нера-во: lim f(x) ≥ lim g(x) Если переменная величина возрастающая и она ограничена, то эта переменная величина имеет предел. Первый замечательный предел Ф-ция Доказательство:
Рассморим окружность единичного радиуса: OA=OB=1, Sтр. ОBА=1/2 ОА*BD=1/2OA*sinx*OB=1/2sinx Sтр. ОСА=1/2 ОА*СА = ½ tg x Sсект.ОВА= 1/2ОА*х=1/2x Из чертежа видно, что Sтр. OBA<S сект.ОВА<Sтр.ОСА; 1/2 sin x<1/2 х<1/2tgx; sin x<х<tgx Разделим все части неравенства на sinx:
Заменяем выражения на обратные
Перейдем к пределу при х→0
Предел переменной Однако, т.к. cos(-x)=cosx и График ф-ции
При х=0 ф-ция не определена, но пределы в точке 0 слева и справа совпадают. Они = 1. Второй замечательный предел Т-ма: Предел переменной величины (1+1/n)n при неограниченном возрастании n, сущ. и равен иррациональному числу е≈2,71…  Определение. Показательную ф-цию ex наз. экспонентой и часто обозначают exp(x)= ex loge наз. натуральным log и обозн. lnx=logex. Установим связь между натур. и десят. log. Для этого воспользуемся равенством: пусть y= lgx=log10x – это значит, что x=10у. Прологарифмируем обе части по основанию е. ln x = ln 10y= y ln10 ln x= 1/M lg x Можно показ., что предел (1) справедлив не только для послед-тей, но и для ф-ций, а именно ln x = ln 10* lg x
Число lg x = M ln x Сделаем замену переменных x=1/y, тогда предел примет вид y=1/x при х→∞, y→0; последний предел может быть записан в виде:
Непрерывность ф-ции Пусть ф-ция y=f(x) определена в некот. окрестности точки х0, включая саму точку х0. Пусть f(x0)=у0, дадим переменной х приращение Δх, тогда переменная y получит приращение Δy=f(x0+Δx)-f(x0)
Определение. Ф-ция y=f(x) наз. непрерывной при x=x0 (или в точке x0 ), если она определена в некот. окрестности точки x0, вкл. саму точку x0 и если сущ. предел:
Другими словами, ф-ция непрерывна, если малым приращениям аргумента Δх соответ. малое приращение ф-ции Δу. Последнее равенство можно переписать в сл. виде:
Т.е., чтобы перейти к пределу непрерыв. ф-ции f(x) при х→х0, достаточно аргумент этой ф-ции заменить на х0. Учитывая очевидное равенство
Последнее равенство означает, что можно переходить к пределу под знаком непрерывной ф-ции, т. е., если ф-ция непрерывна, то знаки ф-ции и предела можно менять местами. Если для некот. ф-ции не выполняется хотя бы 1 из требований непрерывности в некот. точке х0, то ф-ция наз. разрывной в этой точке, а х0 наз. точкой ее разрыва. Разрывность ф-ции графически означ. разрыв ее графика.
Классификация точек разрыв Определение. Если ф-ция f(x) такова, что сущ. конечные пределы В частности, если пределы слева и справа в этой точке совпадают f(x0-0)=f(x0+0), но ф-ция в точке х0 не определена, то точка х0 называется устранимой точкой разрыва (её можно устранить, положив Определение. Все точки разрыва, не являющиеся точками разрыва 1-го рода называются точками разрыва 2-го рода. К точкам разрыва 2-го рода относят точки ∞го разрыва. Используя св-ва пределов можно док-ть следующие утверждения: 1. Сумма 2-ых непрерывных ф-ций – непрерыв. ф –ция; 2. Произведение 2-х непрерывных ф-ций – ф –ция непрерывная; 3. Частное 2-х непрерывных ф-ций – непрерыв. ф –ция, если знаменатель не обращается в 0. 4. Если ф-ция u=u(x) непрерывна в точке х0, а ф-ция у=у(х) непрерывная в точке u0=u(x0), то сложная ф-ция y(u(x)) – непрерывная в точке х0 Используя эти утверждения можно док-ть сл. теорему: Всякая элементарная ф-ция непрерывна в любой точке, в кот. она определена. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 472. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
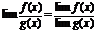 при условии, что lim g(x) ≠0.
при условии, что lim g(x) ≠0. при x→0 имеет предел =1, т.е.
при x→0 имеет предел =1, т.е. 




 заключён м-ду пределами переменных =1. Это возможно если
заключён м-ду пределами переменных =1. Это возможно если  . (док-во для случая x>0)
. (док-во для случая x>0) => доказанный предел будет справедлив также и для отриц. х.
=> доказанный предел будет справедлив также и для отриц. х.
 (1)
(1)

 называется модулем перехода от натур. log к десятичным:
называется модулем перехода от натур. log к десятичным:


 или
или обозначим х= х0+ Δх, тогда при Δх→0 х→х0, тогда имеем:
обозначим х= х0+ Δх, тогда при Δх→0 х→х0, тогда имеем:
 , можем записать:
, можем записать:
 и
и  , но либо ф-ция f(x) не определена в точке х0, либо не все 3 числа f(x0), f(x0-0), f(x0+0) = друг другу, то точка х0 - точка разрыва 1 рода ф-ции f(x).
, но либо ф-ция f(x) не определена в точке х0, либо не все 3 числа f(x0), f(x0-0), f(x0+0) = друг другу, то точка х0 - точка разрыва 1 рода ф-ции f(x). ; после чего, определенная т.о. ф-ция будет непрерывной)
; после чего, определенная т.о. ф-ция будет непрерывной)