Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Нормальное уравнение плоскости и прямой на плоскости.Положение плоскости в пространстве полностью определяется расстоянием от пл-ти (р) до начала координат и единичным вектором
Возьмем произвольную точку М(x,y,z), принадлежащую плоскости. Вектор М0М=r-r0 лежит в этой плоскости и => ^ вектору Т. к. вектор
(4). - норм ур-е пл-ти в коорд. форме. Аналогично можно вывести норм. ур-е прямой на пл-ти:
Норм ур-е прямой в векторной форме будет иметь вид, в точности совпадающий с уравнением (3). Отличия только в том, что входящие в него векторы будут иметь по 2 координаты. Поэтому, расписывая скалярное произведение, имеем норм ур-е прямой в коорд пл-ти:
Уравнения прямой, проходящей через заданную точку параллельно заданному вектору. Положение прямой в пространстве полностью опр-ся некоторой точкой M0(x0,y0,z0), принадлежащей прямой и вектором
Пусть M(x,y,z) произвольная точка прямой. Проведём
Предположим, что направляющий вектор имеет координаты  Аналогично можно получить векторную форму параметрического уравнения прямой на плоскости, которая будет совпадать с уравнением (5):
Входящие сюда векторы имеют по 2 координаты r={x,y}, r0={x0,y0}, S={m,n}. Поэтому в координатной форме получаем 2 параметрических уравнения прямой на плоскости (8):
Канонические уравнения прямой. Исключим параметр t из параметрических уравнений (6) Выражая t из каждого ур-я, мы имеем Приравнивая правые части этих равенств получим каноническое уравнение прямой в пространстве Аналогично, исключая параметр t из системы (8) Уравнение прямой, проходящей через 2 данные точки. Положение прямой в пространстве полностью определяется 2 точками М1(x1,y1,z1) и М2(x2,y2,z2), принадлежащими прямой.
Выбираем в канонич. ур-ях (9) за направляющий вектор
Аналогично из канонического уравнения прямой на пл-ти
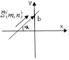
Уравнение прямой на плоскости с угловым коэффициентом. Каноническое уравнение прямой на плоскости Выясним геометр. смысл параметров k и b, входящих в ур-ние y=kx+b
Отсюда вывод, что коэффициент k равен тангенсу угла наклона прямой положительного направления к оси Ох. Он называется угловым коэффициентом прямой. Чтобы выяснить геометр. смысл параметра b найдём ординату точки пересечения прямой с осью Оу. Для этого предположим в ур-ние y=kx+b, что х=0. Тогда получим у=b. Параметр b - ордината точки пересечения прямой с Оу.
|
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 475. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
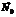 ^ плоскости.
^ плоскости.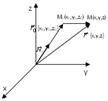
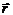 на вектор
на вектор 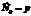 .
. 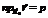
 , то можем записать
, то можем записать 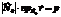 .
. 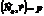
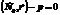 (3) – это норм уравнение плоскости в векторной форме.
(3) – это норм уравнение плоскости в векторной форме. Учитывая, что
Учитывая, что 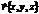 , а
, а 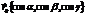 , где
, где 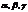 - углы, кот. он образует с коорд. осями Ох, Oy, Oz. Получаем:
- углы, кот. он образует с коорд. осями Ох, Oy, Oz. Получаем: 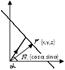

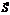 , параллельным прямой.
, параллельным прямой.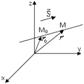
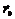 . Тогда вектор
. Тогда вектор 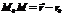 , лежащий на прямой, параллельной направляющему вектору
, лежащий на прямой, параллельной направляющему вектору 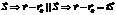
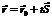 (5) - параметрическое ур-е прямой в пространстве. Число t - параметр. При изменении параметра t от -∞ до +∞ переменная точка, определяемая концом радиус-вектора
(5) - параметрическое ур-е прямой в пространстве. Число t - параметр. При изменении параметра t от -∞ до +∞ переменная точка, определяемая концом радиус-вектора 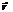 , пробегает положение всех точек прямой.
, пробегает положение всех точек прямой.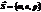 , тогда учитывая, что
, тогда учитывая, что 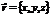 ,
,  из уравнения (5) получаем три уравнения, связывающих соответствующие координаты этих векторов. Параметрическое уравнение прямой в пр-ве в коорд форме: (6)
из уравнения (5) получаем три уравнения, связывающих соответствующие координаты этих векторов. Параметрическое уравнение прямой в пр-ве в коорд форме: (6)
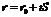 (7).
(7).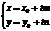
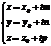

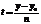
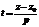
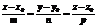 (9).
(9).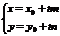 , получим каноническое уравнение прямой на плоскости:
, получим каноническое уравнение прямой на плоскости: 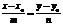
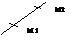
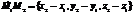 и за фиксированную точку прямой – точку М1(x1,y1,z1).
и за фиксированную точку прямой – точку М1(x1,y1,z1).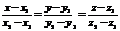 (11)
(11)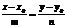 получаем ур-е прямой на пл-ти, проходящей через 2 заданные точки с координатами (x1,y1) и (x2,y2). Оно будет иметь вид (12):
получаем ур-е прямой на пл-ти, проходящей через 2 заданные точки с координатами (x1,y1) и (x2,y2). Оно будет иметь вид (12):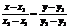
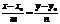 можно переписать в виде
можно переписать в виде 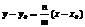 или
или 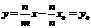 или y=kx+b (13), где
или y=kx+b (13), где 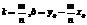
 m и n = проекциям на координатные оси
m и n = проекциям на координатные оси